
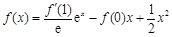 在点
在点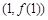 处的切线方程为_________.
处的切线方程为_________. 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:不详 题型:解答题
 为圆心,
为圆心, (
( 为常数,单位为米)为半径的半圆形(如图)荒地,该校总务处计划对其开发利用,其中弓形
为常数,单位为米)为半径的半圆形(如图)荒地,该校总务处计划对其开发利用,其中弓形 区域(阴影部分)用于种植学校观赏植物,
区域(阴影部分)用于种植学校观赏植物, 区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.
区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.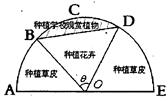
 (单位:弧度),用
(单位:弧度),用 表示弓形
表示弓形 的面积
的面积 ;
;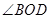 的大小才能使总利润最大?并求出该最大值.
的大小才能使总利润最大?并求出该最大值. ,
, 表示扇形的弧长)
表示扇形的弧长)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,当
,当 时,有
时,有 恒成立,则不等式
恒成立,则不等式 的解集是( )
的解集是( )| A.(-2,0) ∪(2,+∞) | B.(-2,0) ∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com