
A、{x|x<
| ||
B、{x|x<
| ||
C、{x|
| ||
D、{x|x<-1或x>-
|
| 1 |
| 3 |
| 1 |
| 3 |


科目:高中数学 来源: 题型:
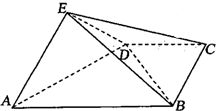 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| A | B | C | D | |
| 身高 | 1.69 | 1.73 | 1.75 | 1.80 |
| 体重指标 | 19.2 | 25.0 | 18.5 | 24.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
 |
| y |
 |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lnx+k |
| ex |
| e-2+1 |
| x2+x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<
已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<| π |
| 2 |
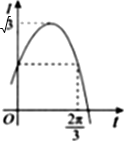
查看答案和解析>>
科目:高中数学 来源: 题型:
 |
| y |
 |
| a |
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:

| A、f(x)-①,g(x)-②,h(x)-③,φ(x)-④ |
| B、f(x)-①,φ(x)-②,g(x)-③,h(x)-④ |
| C、g(x)-①,h(x)-②,f(x)-③,φ(x)-④ |
| D、f(x)-①,h(x)-②,g(x)-③,φ(x)-④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
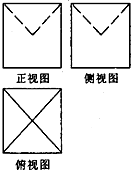 某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com