
分析 (1)根据数列的递推关系结合等比数列的定义进行证明即可,
(2)根据等比数列的通项公式进行求解,
(3)根据分组求和法结合等比数列和等差数列的前n项和公式进行计算即可.
解答 解:(1)∵an+1=-2an-3n-1.
∴n+1+an+1=-2an-3n-1+n+1═-2an-2n=-2(an+1).
则$\frac{{a}_{n+1}+n+1}{{a}_{n}+n}$=-2,
则数列{an+n}为等比数列,公比q=-2;
(2)由(1)得数列{an+n}为等比数列,公比q=-2,首项为a1+1=3+1=4,
则an+n=4•(-2)n-1,
即an=4•(-2)n-1-n,
则数列{an}的通项公式为an=4•(-2)n-1-n;
(3)数列{an}的前n项和Sn=$\frac{4•[1-(-2)^{n}]}{1-(-2)}$-(1+2+…+n)=$\frac{4}{3}$-$\frac{4}{3}$•(-2)n-$\frac{n(n+1)}{2}$.
点评 本题主要考查等比数列的证明以及数列通项公式以及求和公式的应用,利用分组求和法是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 6 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{25}{2}$ | C. | 6 | D. | $\frac{27}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -15 | B. | $-\frac{1}{2}$ | C. | -11 | D. | $-\frac{31}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2-\frac{3}{5}i$ | B. | $2+\frac{3}{5}i$ | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
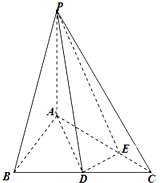 如图,三角形ABC是边长为4的正三角形,PA⊥底面ABC,$PA=\sqrt{7}$,点D是BC的中点,点E在AC上,且DE⊥AC.
如图,三角形ABC是边长为4的正三角形,PA⊥底面ABC,$PA=\sqrt{7}$,点D是BC的中点,点E在AC上,且DE⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com