
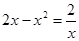 的正根个数为 ( )
的正根个数为 ( )| A.0 | B.1 | C.2 | D.3 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
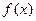 对于其定义域内的某一数
对于其定义域内的某一数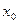 ,有
,有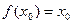 ,则称
,则称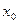 是
是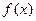 的一个不动点. 已知函数
的一个不动点. 已知函数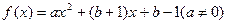 .
.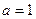 ,
,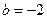 时,求函数
时,求函数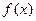 的不动点;
的不动点;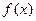 恒有两个不动点,求a的取值范围;
恒有两个不动点,求a的取值范围;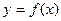
 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数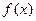 的不动点,且A、B的中点C在函数
的不动点,且A、B的中点C在函数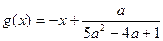 的图象上,求b的最小值.
的图象上,求b的最小值.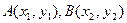 的中点坐标为
的中点坐标为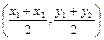 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
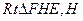 是直角
是直角 顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,
顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,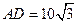 米,记
米,记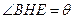 。
。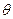 的函数,并写出定义域;
的函数,并写出定义域;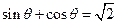 ,求此时管道的长度L;
,求此时管道的长度L;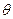 取何值时,污水净化效果最好?并求出此时管道的长度。
取何值时,污水净化效果最好?并求出此时管道的长度。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
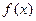 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数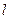 使得对于任意
使得对于任意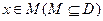 ,有
,有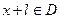 ,且
,且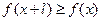 ,则称
,则称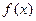 为M上的
为M上的 高调函数如果定义域为R的函数
高调函数如果定义域为R的函数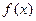 是奇函数,当
是奇函数,当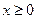 时,
时,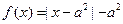 ,且
,且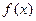 为R上的4高调函数,那么实数
为R上的4高调函数,那么实数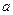 的取值范围是 ( )
的取值范围是 ( )A.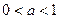 | B.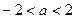 | C.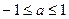 | D.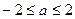 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com