
分析 将要求式子两边乘2(1-$\frac{1}{2}$),运用平方差公式,化简整理,再由数列极限的基本公式,计算即可得到所求值.
解答 解:(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)…(1+$\frac{1}{{2}^{n}}$)
=2(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)…(1+$\frac{1}{{2}^{{2}^{n}}}$)
=2(1-$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)…(1+$\frac{1}{{2}^{{2}^{n}}}$)
=2(1-$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)…(1+$\frac{1}{{2}^{{2}^{n}}}$)
=2(1-$\frac{1}{{2}^{8}}$)(1+$\frac{1}{{2}^{8}}$)…(1+$\frac{1}{{2}^{{2}^{n}}}$)
=…=2(1-$\frac{1}{{2}^{{2}^{n+1}}}$),
则$\underset{lim}{n→∞}$(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)…(1+$\frac{1}{{2}^{{2}^{n}}}$)
=$\underset{lim}{n→∞}$2(1-$\frac{1}{{2}^{{2}^{n+1}}}$)
=2-$\underset{lim}{n→∞}$2•$\frac{1}{{2}^{{2}^{n+1}}}$=2-0=2.
故答案为:2.
点评 本题考查数列极限的求法,注意运用平方差公式,以及常见数列的极限公式,考查化简整理的运算能力,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
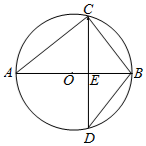 如图,AB是圆O的直径,CD是弦,CD⊥AB于点E,
如图,AB是圆O的直径,CD是弦,CD⊥AB于点E,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com