
���� ��1�����ú���g��x��ͼ���������������б�ʣ��Ӷ�ȷ���е����꣬���������飬���a��b��ֵ��
��2���ٸ��ݷֶκ������������ۣ����ú����ĵ����ԣ�������F��x����[-1��e]�ϵ����ֵ��
�ڸ��ݷֶκ������������ۣ�����$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0��������ʵ��c��ȡֵ��Χ��
��� �⣺��1���ߺ���f��x��=-x3+x2+ax+b����f�䣨x��=-3x2+2x+a��
g��x��=clnx��
�ຯ��g��x����ͼ��������P��1��0����
��x=1ʱ��f�䣨1��=-3+2+a=a-1��
�ֺ���f��x����ͼ���ڵ�P����������ֱ��x-y-4=0��ֱ��
��a-1=-1�����a=0��
��f��1��=-1+1+a+b=0�����b=0��
��2�����ɣ�1��֪��f��x��=-x3+x2��
��x��1ʱ��F��x��=f��x����
��f�䣨x��=-3x2+2x=-x��3x-2����
��f�䣨x��=0�ɵ�x=0��x=$\frac{2}{3}$���ʺ����ڣ�-1��0���ͣ�$\frac{2}{3}$��e���ϵ����ݼ����ڣ�0��$\frac{2}{3}$���ϵ���������
��x��1ʱ��f��x�������ֵΪmax{f��-1����f��$\frac{2}{3}$��}=f��-1��=2��
��1��x��eʱ��F��x��=g��x��=clnx-c��
��c��0����g��x����[1��e]���ǵ��������������ֵ��g��1��=-c��
��c��0����g��x����[1��e]�ϵ�����������g��e��=0��
���ϣ�c��-2ʱ��F��x����[-1��e]�ϵ����ֵΪ2��
c��-2ʱ��F��x����[-1��e]�ϵ����ֵΪ-c��
��F��x��=$\left\{\begin{array}{l}{{-x}^{3}{+x}^{2}��x��1}\\{clnx-c��x��1}\end{array}\right.$��
��������P��Q�ĺ����껥Ϊ�෴����������P��-t��t3+t2����Q��t��f��t��������t��0����
��t��1����f��t��=-t3+t2��
�ɡ�POQ��ֱ�ǵã�$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0����-t2+��t3+t2����-t3+t2��=0��
��t4-t2+1=0����ʱ�⣻
��t��1����f��t��=clnt-c��
����PQ���е���y���ϣ��ҡ�POQ��ֱ�ǣ�����Q�㲻������x���ϣ���t��1��
ͬ����$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0����-t2+��t3+t2��•��clnt-c��=0����c=$\frac{1}{��t+1����lnt-1��}$��
���ں���h��t��=$\frac{1}{��t+1����lnt-1��}$��t��1����ֵ���ǣ�-1��0���ȣ�0��+�ޣ���
����ʵ��c��ȡֵ��Χ�ǣ�-1��0���ȣ�0��+�ޣ���
���� ���⿼���˵������ۺ�Ӧ�����⣬Ҳ�����˺�������ֵ��������۵���ѧ˼�룬���������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
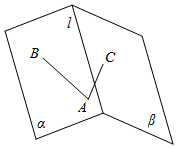 ��ͼ���Զ���Ǧ�-l-��������һ��A�ֱ���AB�ͦ���AC�ͦ£�����ֱ�ΪB��C������BAC=30�㣬�����Ǧ�-l-�µĴ�СΪ150�㣮
��ͼ���Զ���Ǧ�-l-��������һ��A�ֱ���AB�ͦ���AC�ͦ£�����ֱ�ΪB��C������BAC=30�㣬�����Ǧ�-l-�µĴ�СΪ150�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
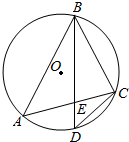 ��ͼ����O�ǡ�ABC�����Բ��D��$\widehat{AC}$���е㣬BD��AC�ڵ�E��
��ͼ����O�ǡ�ABC�����Բ��D��$\widehat{AC}$���е㣬BD��AC�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
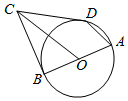 ��ͼ��ʾ��AB��ԲO��ֱ����BC��ԲO������B����ADC+��DCO=180��
��ͼ��ʾ��AB��ԲO��ֱ����BC��ԲO������B����ADC+��DCO=180���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
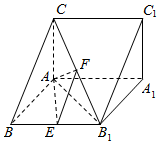 ��֪������ABC-A1B1C1��ͼ��ʾ������CA��ƽ��ABB1A1���ı���ABB1A1Ϊ���Σ���AA1B1=60�㣬EΪBB1���е㣬FΪCB1���е㣮
��֪������ABC-A1B1C1��ͼ��ʾ������CA��ƽ��ABB1A1���ı���ABB1A1Ϊ���Σ���AA1B1=60�㣬EΪBB1���е㣬FΪCB1���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com