解:(1)△APB中,由余弦定理得:AB|
2=|PA|
2+|PB|
2-2|PA|•|PB|•cos2θ=
|PA|
2+|PB|
2-2|PA|•|PB|•(1-2sin
2θ)=|PA|
2+|PB|
2-2|PA|•|PB|+4|PA|•|PB|sin
2θ
=(|PA|-|PB|)
2+8=16,∴||PA|-|PB||=2

,故点P的轨迹是以A、B为焦点的双曲线,
且 c=2,a=

,∴b=

,故双曲线方程为 x
2-y
2=2.
(2)假设存在定点C(m,0),使得
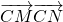
为常数,当直线l斜率存在时,设直线l的方程为 y=k(x-2),
代入双曲线方程得 (1-k
2) x
2+4k
2x-(4k
2+2)=0,由题意知 k≠±1.
∴x
1+x
2=
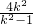
,x
1•x
2=
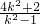
.
∵
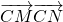
=(x
1-m)(x
2-m)+k
2(x
1-2 )(x
2-2)
=(1+k
2)x
1•x
2-(2k
2+m)(x
1+x
2)+4k
2+m
2=
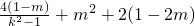
为常数,与k无关,
∴m=1,此时,
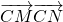
=-1.
当当直线l斜率不存在时,M(2,2

),N (2,-2

),
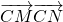
=-1.
综上,存在定点C(1,0),使得
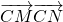
为常数.
分析:(1)△APB中,由余弦定理和已知条件得||PA|-|PB||=2

,再利用双曲线的定义知点P的轨迹是以A、B为焦点的双曲线,求出 a和 b 的值,即得双曲线方程.
(2)假设存在定点C(m,0),用点斜式设出直线l的方程代入双曲线方程,利用根与系数的关系以及
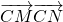
为常数,求得 m 值.
点评:本题考查余弦定理、双曲线的定义,一元二次方程根与系数的关系,向量坐标形式的运算,求定点C 的横坐标m值是解题的难点和关键.

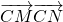 为常数.若存在,求出点C的坐标;若不存在,说明理由.
为常数.若存在,求出点C的坐标;若不存在,说明理由. ,故点P的轨迹是以A、B为焦点的双曲线,
,故点P的轨迹是以A、B为焦点的双曲线, ,∴b=
,∴b= ,故双曲线方程为 x2-y2=2.
,故双曲线方程为 x2-y2=2.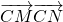 为常数,当直线l斜率存在时,设直线l的方程为 y=k(x-2),
为常数,当直线l斜率存在时,设直线l的方程为 y=k(x-2),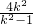 ,x1•x2=
,x1•x2=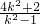 .
.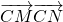 =(x1-m)(x2-m)+k2(x1-2 )(x2-2)
=(x1-m)(x2-m)+k2(x1-2 )(x2-2)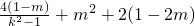 为常数,与k无关,
为常数,与k无关,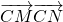 =-1.
=-1. ),N (2,-2
),N (2,-2 ),
),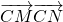 =-1.
=-1.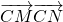 为常数.
为常数. ,再利用双曲线的定义知点P的轨迹是以A、B为焦点的双曲线,求出 a和 b 的值,即得双曲线方程.
,再利用双曲线的定义知点P的轨迹是以A、B为焦点的双曲线,求出 a和 b 的值,即得双曲线方程.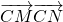 为常数,求得 m 值.
为常数,求得 m 值.
