
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源:2016-2017学年广东省湛江市高一上学期期末调研考试数学试卷(解析版) 题型:填空题
已知点 是直线
是直线 (
( )上一动点,
)上一动点, 、
、 是圆
是圆 :
: 的两条切线,
的两条切线, 、
、 是切点,若四边形
是切点,若四边形 的最小面积是
的最小面积是 ,则
,则 ______.
______.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山东省淄博市高二上学期期末考试数学(理)试卷(解析版) 题型:解答题
某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山东省淄博市高二上学期期末考试数学(理)试卷(解析版) 题型:选择题
命题 :若
:若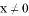 或
或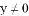 ,则
,则 ,如果把命题
,如果把命题 视为原命题,那么原命题、逆命题、否命题、逆否命题四个命题中正确命题的个数为
视为原命题,那么原命题、逆命题、否命题、逆否命题四个命题中正确命题的个数为
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源:2017届安徽省宿州市高三第一次教学质量检测(期末)文数试卷(解析版) 题型:解答题
设 、
、 分别是椭圆
分别是椭圆 的左、右焦点,
的左、右焦点, 是椭圆
是椭圆 上的点,且
上的点,且 ,坐标原点
,坐标原点 到直线
到直线 的距离是
的距离是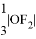 .
.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)过椭圆 的上顶点
的上顶点 作斜率为
作斜率为 的直线
的直线 交椭圆
交椭圆 于另一点
于另一点 ,点
,点 在椭圆
在椭圆 上,且
上,且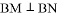 ,求证:存在
,求证:存在 ,使得
,使得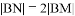 .
.
查看答案和解析>>
科目:高中数学 来源:2017届陕西省西安市高三模拟(一)数学(文)试卷(解析版) 题型:选择题
公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的 值为( )
值为( )
参考数据: ,
, ,
, .
.

A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com