练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    当x∈[－1，3]时，不等式a≥x2－2x－1恒成立，则a的最大值和最小值分别为(    )

    A．2，－1
    B．不存在，2

    C．2，不存在
    D．－2，不存在

    答案：B
    提示：

    由函数图像分析可知．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f（x）=loga（x-3a）（a＞0，且a≠1），当点P（x，y）是函数y=f（x）图象上的点时，点Q（x-2a，-y）是函数y=g（x）图象上的点．
    （1）写出函数y=g（x）的解析式；
    （2）若当x∈[a+2，a+3]时，恒有|f（x）-g（x）|≤1，试确定a的取值范围；
    （3）把y=g（x）的图象向左平移a个单位得到y=h（x）的图象，函数F（x）=2a1-h（x）-a2-2h（x）+a-h（x），（a＞0，且a≠1）在[
    1
    4
    ，4]    的最大值为
    5
    4
    ，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设X～N（μ，O-2），当x在（1，3]内取值的概率与在（5，7]内取值的概率相等时，μ=（　　）

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年河南省洛阳市高三上学期期末考试理科数学 题型：选择题

    已知函数f（x）是定义在R上的以4为周期的函数，”当x∈（－1，3]时，f（x）＝

         其中t>0．若函数y＝－的零点个数是5，则t的取值范

    围为

    A．（，1）     B．（，）      C．（1，）       D．（1，＋∞） 

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)的定义域为［0,1］,且满足下列条件:

    ①对于任意x∈［0,1］,总有f(x)≥3,且f(1)=4;

    ②若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.

    (1)求f(0)的值;

    (2)求证:f(x)≤4;

    (3)当x∈(］(n=1,2,3,…)时,试证明f(x)＜3x+3.

    (文)如图,设抛物线y2=2px(p＞0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1)、(x2,y2),y1＞0,y2＜0,P是此抛物线的准线上的一点,O是坐标原点.

    (1)求证:y1y2=-p2;

    (2)直线PA、PF、PB的方向向量为(1,a)、(1,b)、(1,c),求证:实数a、b、c成等差数列;

    (3)若=0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.

    查看答案和解析>>

    科目：高中数学 来源：2011届河南省洛阳市高三上学期期末考试理科数学 题型：单选题

    已知函数f（x）是定义在R上的以4为周期的函数，”当x∈（－1，3]时，f（x）＝
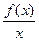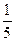     其中t>0．若函数y＝－的零点个数是5，则t的取值范
    围为

    A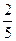．（，1）B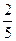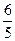．（，）C．（1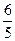，）D．（1，＋∞）

    查看答案和解析>>

    同步练习册答案