
①对于任意x∈[0,1],总有f(x)≥3,且f(1)=4;
②若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.
(1)求f(0)的值;
(2)求证:f(x)≤4;
(3)当x∈(![]() ](n=1,2,3,…)时,试证明f(x)<3x+3.
](n=1,2,3,…)时,试证明f(x)<3x+3.
(文)如图,设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1)、(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,O是坐标原点.

(1)求证:y1y2=-p2;
(2)直线PA、PF、PB的方向向量为(1,a)、(1,b)、(1,c),求证:实数a、b、c成等差数列;
(3)若![]() =0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.
=0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.
(1)解:令x1=x2=0,
由①对于任意x∈[0,1],总有f(x)≥3,
∴f(0)≥3.
又由②得f(0)≥2f(0)-3,
即f(0)≤3;
∴f(0)=3.
(2)证明:任取x1、x2∈[0,1],且设x1<x2,
则f(x2)=f[x1+(x2-x1)]≥f(x1)+f(x2-x1)-3,
∵0<x2-x1≤1,∴f(x2-x1)≥3,
即f(x2-x1)-3≥0.
∴f(x1)≤f(x2).
∴当x∈[0,1]时,f(x)≤f(1)=4.
(3)证明:先用数学归纳法证明
f(![]() )≤
)≤![]() +3(n∈N*).
+3(n∈N*).
(1)当n=1时,f(![]() )=f(1)=4=1+3=
)=f(1)=4=1+3=![]() +3,不等式成立;
+3,不等式成立;
(2)假设当n=k时,f(![]() )≤
)≤![]() +3(k∈N*),
+3(k∈N*),
由f(![]() )=f[
)=f[![]() +(
+(![]() +
+![]() )]
)]
≥f(![]() )+f(
)+f(![]() +
+![]() )-3
)-3
≥f(![]() )+f(
)+f(![]() )+f(
)+f(![]() )-6
)-6
得3f(![]() )≤f(
)≤f(![]() )+6≤
)+6≤![]() +9.
+9.
∴f(![]() )≤
)≤![]() +3,
+3,
即当n=k+1时,不等式成立.
由(1)(2),可知不等式f(![]() )≤
)≤![]() +3对一切正整数都成立.
+3对一切正整数都成立.
于是,当x∈(![]() ,
,![]() ](n=1,2,3,…)时,3x+3>3×
](n=1,2,3,…)时,3x+3>3×![]() +3=
+3=![]() +3≥f(
+3≥f(![]() ),
),
而x∈[0,1],f(x)单调递增,
∴f(![]() )<f(
)<f(![]() ).
).
∴f(x)<f(![]() )<3x+3.
)<3x+3.
(文)证明:(1)①当直线AB的斜率不存在时,设直线AB的方程为x=![]() ,则A(
,则A(![]() ,p),B(
,p),B(![]() ,-p),
,-p),
∴y1y2=-p2.
②当直线AB的斜率存在且不为0时,设直线AB的方程为y=k(x![]() ),
),
则由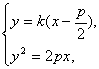 可得ky2-2py-kp2=0(k≠0).∴y1y2=-p2.
可得ky2-2py-kp2=0(k≠0).∴y1y2=-p2.
(2)由已知a=kPA,b=kPF,c=kPB,
设P(![]() ,t),F(
,t),F(![]() ,0),
,0),
∴a=![]() ,b=
,b=![]() ,c=
,c=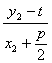 ;
;
且x1=![]() ,x2=
,x2=![]() .
.
故a+c=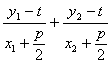
=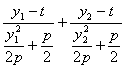
![]()
=![]()
=![]()
=![]() .
.
∴a、b、c成等差数列.
(3)证法一:∵![]() =0,
=0,
∴PA⊥PB,故a·c=-1.
由(2)可知a+c=2b,即a-b=b-c.
①若AB⊥x轴,则α=β=45°,θ=0°,
∴θ=α-β.
②若kAB>0,则
tanα=![]() .
.
同理可得tanβ=a,
∴tan(α-β)=![]() ,
,
即|tan(α-β)|=|b|=tanθ.
易知∠PFO、∠BPF、∠APF都是锐角.
∴θ=|α-β|.
③若kAB<0,类似地,也可证明θ=|α-β|.
综上所述,θ=|α-β|.
证法二:∵![]() =0,∴PA⊥PB.
=0,∴PA⊥PB.
故a·c=-1.
①如图,若AB⊥x轴,则α=β=45°,θ=0°,
∴θ=α-β.

②若kAB>0,∵A、B在抛物线上,
∴|AF|=|AC|,|BF|=|BD|.
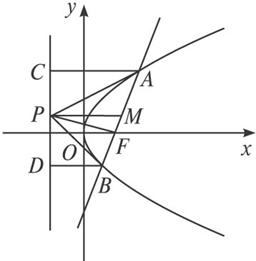
设AB中点为M,则
|PM|=![]() ,
,
∴PM是梯形ABDC的中位线,
故P是CD中点.
∴P(![]() ),t=
),t=![]() ,
,
F(![]() ,0),
,0),
![]() =(p,
=(p,![]() ),
),
又![]() =(x2-x1,y2-y1),
=(x2-x1,y2-y1),
∴![]() =p(x2-x1)
=p(x2-x1)![]()
=p(x2-x1)![]() =0.
=0.
∴![]() .
.
∴△PDB≌△PBF.
∴∠BPF=∠DPB=β.
∴θ+2β=90°=α+β.∴θ=α-β.
③若kAB<0,类似②可证θ=β-α,
∴θ=|α-β|.


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| a-3 |
| 2 |
| x | 2 1 |
| x | 2 2 |
| x | 3 1 |
| x | 3 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 1+x |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| x |
| ||
1+
|
| x |
| 1+x |
| 1 |
| 1+x |
| x |
| 1+x |
| 1+x |
| 1+x |
| 1 | ||
2x+
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 1-x |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| lim |
| n→∞ |
| 4Sn-9Sn |
| 4Sn+1+9Sn+1 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+1-a |
| a-x |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sinα | ||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com