练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数
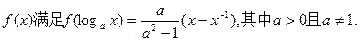
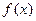    （1）求函数的解析式，并指出其单调性；
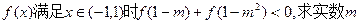    （2）函数的取值集合；
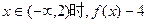    （3）当的值恰为负数，求a的取值范围。
    见解析
    解：（1）令
    的定义域为R。 ………………3分
    为奇函数。

    综上，为R上的增函数。  ………………5分
    （2）由得：  
    再由定义域和单调性得：，解之得： 
    （3）因为在R上是增函数，且…………10分
    要使在上恰为负数，只需，
    解之得  ………………12分
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

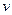    在固定压力差（压力差为常数）下，当气体通过圆形管道时，其流量速率（单位：cm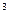/s）与管道半径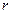（单位：cm）的四次方成正比．
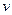    （１）  写出气流速度关于管道半径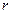的函数解析式；
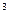    （２）  若气体在半径为3cm的管道中，流量速率为400cm/s，求该气体通过半
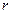    径为的管道时，其流量速率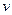的表达式；
    （３）  已知（２）中的气体通过的管道半径为5cm，计算该气体的流量速率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

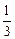     如果函数f(x)在R上为奇函数，在(－1，0)上是增函数，且f(x+2)=－f(x),试比较f(),f(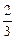),f(1)的大小关系_________. 

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题12分）已知函数（I）当a=1时，求的最小值；（II）若恒成立，求a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分13分)
    某化工企业生产某种产品，生产每件产品的成本为3元，根据市场调查，预计每件产品的出厂价为x元(7≤x≤10)时，一年的产量为(11 – x)2万件；若该企业所生产的产品能全部销售，则称该企业正常生产；但为了保护环境，用于污染治理的费用与产量成正比，比例系数为常数a (1≤a≤3)．
    （Ⅰ）求该企业正常生产一年的利润L (x)与出厂价x的函数关系式；       
    （Ⅱ）当每件产品的出厂价定为多少元时，企业一年的利润最大，并求最大利润．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    集合A={3，4}，B={5，6，7}，那么可建立从A到B的映射个数是__________，从B到A的映射个数是__________.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    定义在R上的奇函数有最小正周期4，且时，。求在上的解析式

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

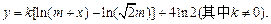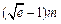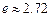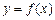    （本题满分13分）已知火箭的起飞重量M是箭体（包括搭载的飞行器）的重量m和燃料重量x之和.在不考虑空气阻力的条件下，假设火箭的最大速度y关于x的函数关系式为：当燃料重量为吨（e为自然对数的底数，）时，该火箭的最大速度为4（km/s）.（Ⅰ）求火箭的最大速度与燃料重量x吨之间的函数关系式；（Ⅱ）已知该火箭的起飞重量是544吨，是应装载多少吨燃料，才能使该火箭的最大飞行速度达到8km/s，顺利地把飞船发送到预定的轨道？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    函数的值域是__________ 

    查看答案和解析>>

    同步练习册答案