
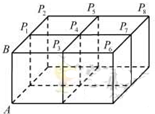
 如图,四个棱长为1的正方体排成一个正四棱柱,AB是一条侧棱,Pi(i=1,2,…8)是上底面上其余的八个点,则
如图,四个棱长为1的正方体排成一个正四棱柱,AB是一条侧棱,Pi(i=1,2,…8)是上底面上其余的八个点,则| AB |
| APi |
| A、1 | B、2 | C、3 | D、4 |
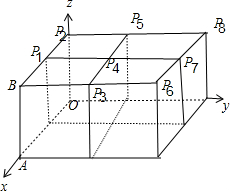 解:如图建立空间直角坐标系,
解:如图建立空间直角坐标系,| AB |
| AP1 |
| AP2 |
| AP3 |
| AP4 |
| AP5 |
| AP6 |
| AP7 |
| AP8 |
| AB |
| APi |
| AB |
| APi |


科目:高中数学 来源: 题型:
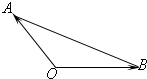 若Ai(i=1,2,3,…,n)是△AOB所在的平面内的点,且
若Ai(i=1,2,3,…,n)是△AOB所在的平面内的点,且| OAi |
| OB |
| OA |
| OB |
| OA1 |
| OA2 |
| OAn |
| OA |
| OAi |
| OB |
| OA |
| OAi |
| OB |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
| 4 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:解答题
设在一个盒子中,放有标号为1,2,3的三张卡片,现从这个盒子里有放回地先后抽得两张卡片,标号分别记为x,y,设随机变量ξ=|x-2|+|y-x|
(1)写出随机变量ξ的取值集合(直接写出答案即可);
(2)求ξ的分布列和数学期望及方差.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:解答题
某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为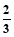 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为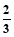 、
、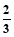 、
、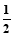 ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(1)求随机变量ξ的分布列和数学期望;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分” 这一事件,求P(AB).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com