【答案】
分析:(1)由直线与抛物线联立方程组解得A(16,-8),B(0,0),由点斜式写出两条直线l
1、l
2的方程,从而得出直线AB的斜率;
(2)推广的评分要求分三层:
一层:点P到一般或斜率到一般,或抛物线到一般,例子:1、已知A、B是抛物线y
2=4x上的相异两点.设过点A且斜率为-1的直线l
1,与过点B且斜率为1的直线l
2相交于抛物线y
2=4x上的一定点P
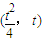
,求直线AB的斜率等等;
二层:两个一般或推广到其它曲线;
三层:满分(对抛物线,椭圆,双曲线或对所有圆锥曲线成立的想法)
(3)点Q(x
,0),设A(x
1,y
1),B(x
2,y
2),则y
i2=4x
i(i=1,2).设线段AB的中点是M(x
m,y
m),斜率为k,写出线段AB的垂直平分线l的方程,又点Q(5,0)在直线l上,求出x
m=3.最后利用0<y
m2<4x
m=12,即可求出中点的纵坐标的取值范围.
解答:解:(理)(1)由
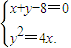
解得A(16,-8);由
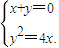
解得B(0,0).
由点斜式写出两条直线l
1、l
2的方程,l
1:x+y-8=0;l
2:x-y=0,所以直线AB的斜率为
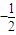
. …(4分)
(2)推广的评分要求分三层
一层:点P到一般或斜率到一般,或抛物线到一般((3分),问题(1分)、解答2分)
例:1、已知A、B是抛物线y
2=4x上的相异两点.设过点A且斜率为-1的直线l
1,与过点B且斜率为1的直线l
2相交于抛物线
y
2=4x上的一定点P
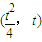
,求直线AB的斜率;
2、已知A、B是抛物线y
2=4x上的相异两点.设过点A且斜率为-k 1的直线l
1,与过点B且斜率为k的直线l
2相交于抛物线
y
2=4x上的一点P(4,4),求直线AB的斜率;
3、已知A、B是抛物线y
2=2px(p>0)上的相异两点.设过点A且斜率为-1的直线l
1,与过点B且斜率为1的直线l
2相交于抛物线y
2=2px(p>0)上的一定点P
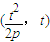
,求直线AB的斜率; AB的斜率的值.
二层:两个一般或推广到其它曲线((4分),问题与解答各占2分)
例:4.已知点Ρ是抛物线y
2=4x上的定点.过点P作斜率分别为k、-k的两条直线l
1、l
2,分别交抛物线于A、B两点,试计算直线AB的斜率.
三层:满分(对抛物线,椭圆,双曲线或对所有圆锥曲线成立的想法.)((7分),问题(3分)、解答4分)
例如:5.已知抛物线y
2=2px上有一定点P,过点P作斜率分别为k、-k的两条直线l
1、l
2,分别交抛物线于A、B两点,试计算直线AB的斜率.
过点P(x
,y
),斜率互为相反数的直线可设为y=k(x-x
)+y
,y=k(x-x
)+y
,其中y
2=2px
.
由
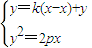
得ky
2-2py+2py
-ky
2=0,所以
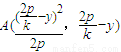
同理,把上式中k换成-k得
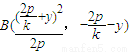
,所以
当P为原点时直线AB的斜率不存在,当P不为原点时直线AB的斜率为
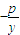
.
(3)点Q(x
,0),设A(x
1,y
1),B(x
2,y
2),则y
i2=4x
i(i=1,2).
设线段AB的中点是M(x
m,y
m),斜率为k,则
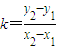
=
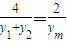
.(12分)
所以线段AB的垂直平分线l的方程为
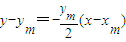
,
又点Q(5,0)在直线l上,所以
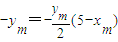
,
而y
m≠0,于是x
m=3. …(13分)
(斜率

,
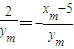
,则x
m=3 (13分)
线段AB所在直线的方程为
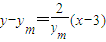
,…(14分)
代入y
2=4x,整理得4x
2-24x+y
m4-12y
m2+36=0…(15分)x
1+x
2=6,
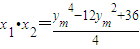
.
设AB线段长为l,则
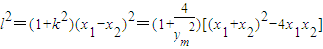
=(4+y
m2)(-y
m2+12)=-y
m4+8y
m2+48…(16分)
因为0<y
m2<4x
m=12,所以
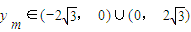
…(18分)
即:
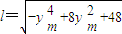
.(
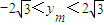
).
点评:本小题主要考查抛物线的简单性质、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

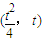 ,求直线AB的斜率等等;
,求直线AB的斜率等等;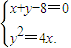 解得A(16,-8);由
解得A(16,-8);由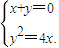 解得B(0,0).
解得B(0,0).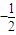 . …(4分)
. …(4分)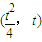 ,求直线AB的斜率;
,求直线AB的斜率;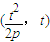 ,求直线AB的斜率; AB的斜率的值.
,求直线AB的斜率; AB的斜率的值.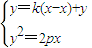 得ky2-2py+2py-ky2=0,所以
得ky2-2py+2py-ky2=0,所以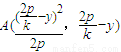
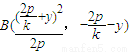 ,所以
,所以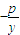 .
.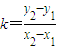 =
=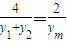 .(12分)
.(12分)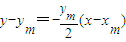 ,
,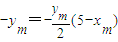 ,
, ,
,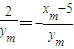 ,则xm=3 (13分)
,则xm=3 (13分)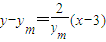 ,…(14分)
,…(14分)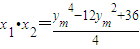 .
.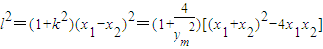
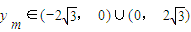 …(18分)
…(18分)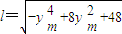 .(
.(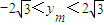 ).
).

 •
• =0,则原点O到直线AB的最大距离为( )
=0,则原点O到直线AB的最大距离为( )