
(本小题满分12分)已知二次函数 对任意实数
对任意实数 都满足
都满足 ,且
,且 .令
.令 .
.
(1)若函数 在
在 上的最小值为0,求
上的最小值为0,求 的值;
的值;
(2)记函数 ,若函数
,若函数 有5个不同的零点,求实数
有5个不同的零点,求实数 的取值范围.
的取值范围.
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源:2014-2015年河北保定一中高二下第一次段考理数学试卷(解析版) 题型:选择题
设点 是曲线:
是曲线: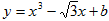 (
( 为实常数)上任意一点,
为实常数)上任意一点, 点处切线的倾斜角为
点处切线的倾斜角为 ,则
,则 的取值范围是( )
的取值范围是( )
A. B.
B.
C.[0, ]∪
]∪ D.[0,
D.[0, )∪
)∪
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上学期期中文科数学试卷(解析版) 题型:解答题
(本小题满分12分)设向量 ,其中
,其中 ,
, ,已知函数
,已知函数 的最小正周期为
的最小正周期为 .
.
(1)求 的对称中心;
的对称中心;
(2)若 是关于
是关于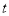 的方程
的方程 的根,且
的根,且 ,求
,求 的值.
的值.
【答案】(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先利用两角和与差的正弦化简函数的解析式,再根据函数最小正周期求得函数的解析式,由此求得函数的对称中心;(2)先根据方程根的概念求得 的值,再由
的值,再由 的范围求得
的范围求得 的值,从而代入函数解析式中求得
的值,从而代入函数解析式中求得 的值.
的值.
试题解析:(1) 

又  , 得
, 得  所以
所以  对称中心为
对称中心为 
(2)由 得
得  或
或  即
即 或
或 ,又
,又
所以 ,得
,得 ,故
,故
考点:1、两角两角和与差的正弦;2、三角函数的周期;3、特殊三角形函数的值.
【规律点睛】平面向量与三角函数的综合,通常利用平面向量的垂直、平行、数量积公式等知识将向量问题转化为三角函数问题,再结合三角知识求解.而求三角函数的最值(值域)、单调性、奇偶性、对称性,通常要将函数的解析式转化为 的形式,然后利用整体思想求解.
的形式,然后利用整体思想求解.
【题型】解答题
【适用】较难
【标题】【百强校】2016届江西省临川一中高三上学期期中文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分12分)在四棱柱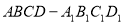 中,
中, ,底面
,底面 为菱形,
为菱形,
 ,已知
,已知 .
.

(1)求证:平面 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高三周练数学试卷(解析版) 题型:解答题
已知 .
.
(1)求 的单调区间;
的单调区间;
(2)令 ,则
,则 时有两个不同的根,求
时有两个不同的根,求 的取值范围;
的取值范围;
(3)存在 ,
, 且
且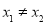 ,使
,使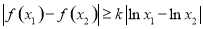 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届甘肃省高三上学期期中文科数学试卷(解析版) 题型:填空题
在△ABC中,AB=2,BC=3,∠ABC=60°,AD为BC边上的高,O为AD的中点,若 =λ
=λ +μ
+μ ,则λ+μ
,则λ+μ ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com