【题目】已知圆
，直线
.
（1）判断直线
与圆C的位置关系；
（2）若定点P（1，1）分弦AB为
，求此时直线的方程.
【答案】（1）相交（2）
或
.
【解析】
试题分析：（1）由圆的方程得到圆心坐标和半径，然后由点到直线的距离公式得到圆心到直线的距离，利用不等式放缩后得到圆心到直线的距离和半径的关系，从而得到答案；（2）把线段的长度比转化为两个想两件的关系，由向量的坐标运算得到A，B两点横坐标间的关系，联立直线与圆的方程化为关于x的一元二次方程，由根与系数关系得到A，B两点横坐标的和，求出其中一点的横坐标，最后再代入关于x的方程得到关于m的方程，求解得到m的值，则直线方程可求
试题解析：（1）圆
的圆心为
，半径为
。
∴圆心C到直线
的距离
∴直线
与圆C相交；
（2）设
，由
得，
∴
，化简的
………①
又由
消去
得
……（*）
∴
…………②
由①②解得
，带入（*）式解得
，
∴直线
的方程为或.
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目：高中数学 来源： 题型：
【题目】下列说法中错误的是（ ）
A.在三角形中，已知两边及其一边的对角，不能用余弦定理求解三角形
B.余弦定理揭示了任意三角形边角之间的关系，因此它适用于任何三角形
C.利用余弦定理，可以解决已知三角形三边求角的问题
D.在三角形中，勾股定理是余弦定理的特例
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，过点
的直线与抛物线
相交于点
，
两点，设
，
（1）求证：
为定值
（2）是否存在平行于
轴的定直线被以
为直径的圆截得的弦长为定值？如果存在，求出该直线方程和弦长，如果不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地政府为科技兴市，欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区．已知
，
，
，曲线
是以点
为顶点的且开口向上的抛物线的一段，如果要使矩形的相邻两边分别落在
，
上，且一个顶点落在曲线段
上，问矩形的两边长分别为多少时使矩形工业园区的用地面积最大？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在三棱锥A－BOC中，OA⊥底面BOC，∠OAB＝∠OAC＝30°，AB＝AC＝4，BC＝
，动点D在线段AB上.
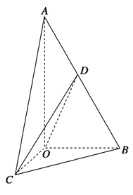
（1）求证：平面COD⊥平面AOB；
（2）当OD⊥AB时，求三棱锥C－OBD的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一次篮球定点投篮训练中，规定每人最多投3次，在
处每投进一球得3分；在
处每投进一球得2分．如果前两次得分之和超过3分就停止投篮；否则投第三次．某同学在
处的投中率
，在
处的投中率为
，该同学选择先在
处投第一球，以后都在
处投，且每次投篮都互不影响，用
表示该同学投篮训练结束后所得的总分，其分布列为：
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
（1）求
的值；
（2）求随机变量
的数学期望
；
（3）试比较该同学选择上述方式投篮得分超过3分与选择都在
处投篮得分超过3分的概率的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
