
【题目】已知等腰三角形△ABC的两腰AB和AC所在直线的方程分别为![]() 和
和![]()
![]() 是底边BC上一点,求:
是底边BC上一点,求:
(1)底边BC所在直线的方程;
(2)△ABC的面积.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的.在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点![]() ,
,![]() ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”:![]() ;到两点P.Q“距离”相等的点的轨迹称为线段PQ的“垂直平分线”.已知点
;到两点P.Q“距离”相等的点的轨迹称为线段PQ的“垂直平分线”.已知点![]() 、
、![]() 、
、![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]()
![]() 上一点
上一点![]() 到原点
到原点![]() 的“距离”;
的“距离”;
(2)写出线段AB的“垂直平分线”的轨迹方程,并作出大致图像;
(3)定义:若三角形三边的“垂直平分线”交于一点,则该点称为三角形的“外心”.试判断![]() 的“外心”是否存在,如果存在,求出“外心”;如果不存在,说明理由.
的“外心”是否存在,如果存在,求出“外心”;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,给出以下结论:①
的两侧,给出以下结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值,无最大值;③
有最小值,无最大值;③![]() ;④当
;④当![]() 且
且![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,正确的个数为( )
,正确的个数为( )
A.1个B.2个C.3个D.以上都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 是棱长为
是棱长为![]() 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有![]() 个顶点;②有
个顶点;②有![]() 条棱;③有
条棱;③有![]() 个面;④表面积为
个面;④表面积为![]() ;⑤体积为
;⑤体积为![]() .其中正确的结论是____________.(要求填上所有正确结论的序号)
.其中正确的结论是____________.(要求填上所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆P恒过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆P圆心的轨迹M的方程;
(Ⅱ)正方形ABCD中,一条边AB在直线y=x+4上,另外两点C、D在轨迹M上,求正方形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在万众创新的大经济背景下,某成都青年面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以![]() 天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为
天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为![]() ,记当日这款新面包获得的总利润为
,记当日这款新面包获得的总利润为![]() (单位:元).求
(单位:元).求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: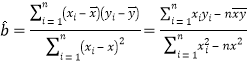 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为常数,且
为常数,且![]() ).
).
(1)若当![]() 时,函数
时,函数![]() 与
与![]() 的图象有且只要一个交点,试确定自然数
的图象有且只要一个交点,试确定自然数![]() 的值,使得
的值,使得![]() (参考数值
(参考数值![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)当![]() 时,证明:
时,证明:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2-2x-4y=0.
(1)求圆C关于直线x-y-1=0对称的圆D的标准方程;
(2)过点P(4,-4)的直线l被圆C截得的弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() 中,AB=3,
中,AB=3,![]() =4,M为
=4,M为![]() 的中点,P是BC边上的一点,且由点P沿棱柱侧面经过棱
的中点,P是BC边上的一点,且由点P沿棱柱侧面经过棱![]() 到M点的最短路线长为
到M点的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]() 的交点为N,求
的交点为N,求
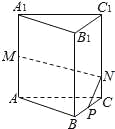
(1)该三棱柱的侧面展开图的对角线长.
(2)PC和NC的长
(3)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com