
 在平面直角坐标系xOy中,椭圆Γ:
在平面直角坐标系xOy中,椭圆Γ:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| x2 |
| 4 |
|
|
| -8k2 |
| 1+4k2 |
| -8k2 |
| 1+4k2 |
| 2k |
| 1+4k2 |
|
| -8k2 |
| 1+4k2 |
| 2k |
| 1+4k2 |
(
| ||
| 4 |
| 2k |
| 1+4k2 |


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
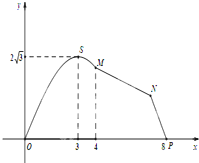 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asin(ωx)(A>0,ω>0),x∈[0,4]的图象,且图象的最高点为S(3,2
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asin(ωx)(A>0,ω>0),x∈[0,4]的图象,且图象的最高点为S(3,2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
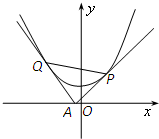 过x轴上动点A(a,0),引抛物线y=x2+1的两条切线AP、AQ.切线斜率分别为k1和k2,切点分别为P、Q.
过x轴上动点A(a,0),引抛物线y=x2+1的两条切线AP、AQ.切线斜率分别为k1和k2,切点分别为P、Q.| S△APQ | ||
|
|
| AP |
| AQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
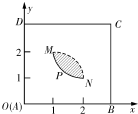 如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=
如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=| 2 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| x |
| 4 |
| b |
| x |
| 4 |
| x |
| 4 |
| a |
| b |
| x |
| 2 |
| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com