
【题目】已知函数![]() 是R上的偶函数,且当x>0时,函数的解析式为
是R上的偶函数,且当x>0时,函数的解析式为![]() =
=![]() .
.
(1)判断并证明![]() 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)求:当x<0时,函数![]() 的解析式.
的解析式.
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:用定义证明函数的单调性需要以下步骤,一、取值,在x>0内任取两个自变量![]() ,且
,且![]() ,二、作差
,二、作差![]() ,三、变形(包括通分、配方、因式分解、分子有理化等),四、断号(判断各部分的正负,说明差的符号正负),最后给出结论.利用函数的奇偶性求函数的解析式是函数的奇偶性的应用之一,给出函数在x>0的解析式,利用当x<0时,-x>0,借助f(x)=f(-x)就可以求出x<0时的解析式;
,三、变形(包括通分、配方、因式分解、分子有理化等),四、断号(判断各部分的正负,说明差的符号正负),最后给出结论.利用函数的奇偶性求函数的解析式是函数的奇偶性的应用之一,给出函数在x>0的解析式,利用当x<0时,-x>0,借助f(x)=f(-x)就可以求出x<0时的解析式;
试题解析:
(1)当![]() 时,
时, ![]()
![]()
![]() 是
是![]() 上减函数
上减函数
证明: ![]() 且
且![]()
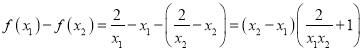
![]()
![]()
![]() 即
即![]()
![]() 是
是![]() 上减函数.
上减函数.
当![]() 时,
时, ![]()
![]() 为R上偶函数
为R上偶函数![]()
![]() 当
当![]() 时,
时, ![]() .
.
【点精】函数的单调性的判断分为“粗判”和“细断”两种,所谓粗判,就是根据已知函数的单调性结合和复合函数关系,判断出函数在某区间上的单调性;所谓细断就是根据函数的单调性定义进行严格证明或利用导数的正负进行严格的判断,关于利用函数的单调性的定义证明,其步骤为①取值,②作差,③变形,④断号,最后给出单调性结论. 利用函数的奇偶性求函数的解析式是函数的奇偶性的应用之一,给出函数在x>0的解析式,利用当xlt;0时,-x>0,偶函数借助f(x)=f(-x)就可以求出x<0时的解析式;


科目:高中数学 来源: 题型:
【题目】某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,
初赛采用选手选一题答一题的方式进行,每位选手最多有![]() 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对![]() 题或答错
题或答错![]() 题即终止其初赛的比赛,答对
题即终止其初赛的比赛,答对![]() 题者直接进入决赛,答错
题者直接进入决赛,答错![]() 题者则被淘汰.已知选手甲答题的正确率为
题者则被淘汰.已知选手甲答题的正确率为![]() .
.
(1) 求选手甲可进入决赛的概率;
(2) 设选手甲在初赛中答题的个数为![]() ,试写出
,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(1-x),g(x)=log2(x+1),设F(x)=f(x)-g(x).
(1)判断函数F(x)的奇偶性;
(2)证明函数F(x)是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解大学生观看浙江卫视综艺节目“奔跑吧兄弟”是否与性别有关,一所大学心理学教师从该校学生中随机抽取了50人进行问卷调查,得到了如下的列联表:
喜欢看“奔跑吧兄弟” | 不喜欢看“奔跑吧兄弟” | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
若该教师采用分层抽样的方法从50份问卷调查中继续抽查了10份进行重点分析,知道其中喜欢看“奔跑吧兄弟”的有6人.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜欢看“奔跑吧兄弟”节目与性别有关?说明你的理由;
的把握认为喜欢看“奔跑吧兄弟”节目与性别有关?说明你的理由;
(3)已知喜欢看“奔跑吧兄弟”的10位男生中,![]() 还喜欢看新闻,
还喜欢看新闻,![]() 还喜欢看动画片,
还喜欢看动画片,![]() 还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求
还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
P(χ2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数![]() 在区间
在区间![]() 上是增函数,且最大值为10,最小值为4,则在区间
上是增函数,且最大值为10,最小值为4,则在区间![]() 上
上![]() 的最大值、最小值分别是( )
的最大值、最小值分别是( )
A. -4,-10 B. 4,-10
C. 10,4 D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使![]() =
=![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
⑴当![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 内有两个不同的不动点,求实数
内有两个不同的不动点,求实数![]() 的取值范围;
的取值范围;
(3)若对于任意实数![]() ,函数
,函数![]() 恒有两个不相同的不动点,求实数
恒有两个不相同的不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求:
(1)连续取两次都是红球的概率;
(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数![]() 的概率分布列及期望.
的概率分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com