已知命题p:?x∈R,使得k+|x-2|≥|x-1|;命题q:?x,y∈R+且x+y=1,有xyk≤x+4y.若p∧q为真,则实数k的取值范围是( )
A.[-1,9]
B.[1,9]
C.[-1,8]
D.[1,8]
【答案】
分析:本题考查复合命题,解决的方法是:将k+|x-2|≥|x-1|和xyk≤x+4y分别变形后求出k的取值范围,最后求交集.
解答:解:命题p:?x∈R,使得k+|x-2|≥|x-1|成立,
∴有:?x∈R,k≥|x-1|-|x-2|成立,
∴只须:k大于等于(|x-1|-|x-2|)的最小值即可,
而由绝对值的几何意义可知|x-1|-|x-2|表示数轴上的点到1和2的距离之差,

由上图分析得:当实数x在数轴上移动时有:-1≤|x-1|-|x-2|≤1,
即:k≥-1.
命题q:?x,y∈R
+且x+y=1,有xyk≤x+4y,
∴有:
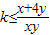
对?x,y∈R
+且满足x+y=1的实数x、y成立,
∴只须:k小于等于
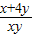
的最小值即可,
而

=

=

=5+
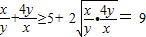
,
即:k≤9.
又∵p∧q为真,
∴命题p和命题q均为真命题,
∴应有
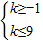
,解得:-1≤k≤9,即:[-1,9].
故选A.
点评:本题以复合命题的真假为载体,主要考查绝对值的几何意义及不等式求函数的最值的掌握情况,要做到熟练掌握.


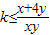 对?x,y∈R+且满足x+y=1的实数x、y成立,
对?x,y∈R+且满足x+y=1的实数x、y成立,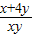 的最小值即可,
的最小值即可, =
= =
= =5+
=5+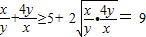 ,
,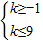 ,解得:-1≤k≤9,即:[-1,9].
,解得:-1≤k≤9,即:[-1,9].
