考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:计算题,三角函数的求值,解三角形
分析:(1)利用向量的数量积运算,根据向量垂直建立方程,即可求得角B的大小;
(2)将函数解析式转化为A的三角函数,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据B的度数,得出A的范围,求出这个角的范围,根据正弦函数的图象与性质求出f(B)取得最大值时A的度数,可得出此时C的度数,进而判断出此三角形为等边三角形;
解答:
解:(1)∵
⊥
,∴
•
=0,
即:(2-2sinB)(1+sinB)+(cosB-sinB)(cosB+sinB)=0,
化简可得3-4sin
2B=0,∴sinB=
,
∵三角形ABC是锐角三角形,
∴B=
.
(2)由(1)可知,B=
,函数y=2sin
2A+cos(
)=2sin
2A+cos(
)
=2sin
2A+cos(
-2A)=-cos2A+
cos2A+
sin2A+1=sin(2A-
)+1.
当2A-
=
时,即A=
时,y有最大值,此时A=B=C,
∴△ABC是正三角形.
点评:考查了两角和与差的三角函数,二倍角的正弦、余弦函数公式,正弦函数的定义域与值域,三角形形状的判断,熟练掌握定理及公式是解本题的关键.



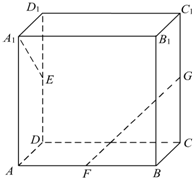 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值是( )
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值是( )