
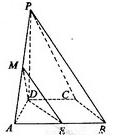
如图,在四棱柱


(I)当正视方向与向量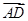 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥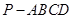 的正视图(要求标出尺寸,并写出演算过程);
的正视图(要求标出尺寸,并写出演算过程);
(II)若M为PA的中点,求证:求二面角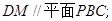
(III)求三棱锥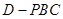 的体积.
的体积.
(I)见解析(II)见解析(III)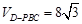
【解析】(Ⅰ)在梯形 中,过点
中,过点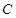 作
作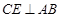 ,垂足为
,垂足为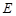 ,
,
由已知得,四边形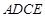 为矩形,
为矩形,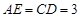
在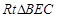 中,由
中,由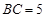 ,
,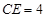 ,依勾股定理得:
,依勾股定理得:
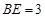 ,从而
,从而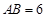
又由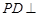 平面
平面 得,
得,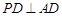
从而在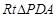 中,由
中,由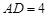 ,
,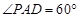 ,得
,得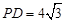
正视图如右图所示:

(Ⅱ)取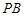 中点
中点 ,连结
,连结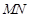 ,
,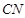
在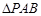 中,
中,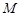 是
是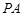 中点,
中点,
∴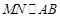 ,
,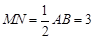 ,又
,又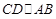 ,
,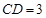
∴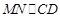 ,
,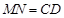
∴四边形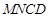 为平行四边形,∴
为平行四边形,∴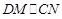
又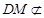 平面
平面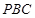 ,
,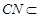 平面
平面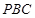
∴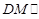 平面
平面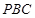

(Ⅲ)
又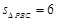 ,
,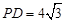 ,所以
,所以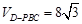
解法二:
(Ⅰ)同解法一
(Ⅱ)取 的中点
的中点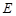 ,连结
,连结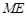 ,
,
在梯形 中,
中,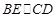 ,且
,且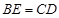
∴四边形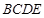 为平行四边形
为平行四边形
∴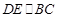 ,又
,又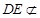 平面
平面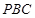 ,
,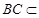 平面
平面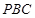
∴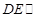 平面
平面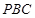 ,又在
,又在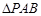 中,
中,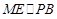
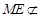 平面
平面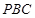 ,
,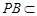 平面
平面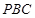
∴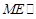 平面
平面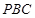 .又
.又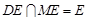 ,
,
∴平面 平面
平面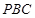 ,又
,又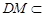 平面
平面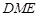
∴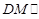 平面
平面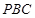
(Ⅲ)同解法一
对于立体几何的考查所有关系的决断往往基于对公理定理推论掌握的比较熟练,又要善于做出一线辅助线加以证明,再者就是体积和表面积的计算公式要熟悉.
【考点定位】 本题主要考查直线与直线、直线与平面的位置关系及几何体的三视图和体积等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想.属容易题


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
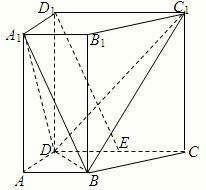 如图,在四棱柱ABCD-A1B1C1D1中,DD1⊥面ABCD已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
如图,在四棱柱ABCD-A1B1C1D1中,DD1⊥面ABCD已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.查看答案和解析>>
科目:高中数学 来源: 题型:
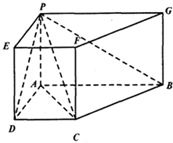
查看答案和解析>>
科目:高中数学 来源: 题型:
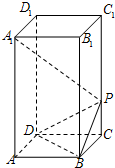 (2013•江门二模)如图,在四棱柱ABCD-A1B1C1D1中,已知底面ABCD是边长为
(2013•江门二模)如图,在四棱柱ABCD-A1B1C1D1中,已知底面ABCD是边长为| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com