
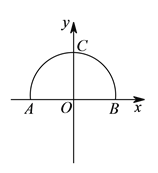
【题目】如图是一段圆锥曲线,曲线与两个坐标轴的交点分别是![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)若该曲线表示一个椭圆,设直线![]() 过点
过点![]() 且斜率是
且斜率是![]() ,求直线
,求直线![]() 与这个椭圆的公共点的坐标.
与这个椭圆的公共点的坐标.
(Ⅱ)若该曲线表示一段抛物线,求该抛物线的方程.
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知内角 ![]() ,边
,边 ![]() .设内角B=x,△ABC的面积为y.
.设内角B=x,△ABC的面积为y.
(1)求函数y=f(x)的解析式和定义域;
(2)当角B为何值时,△ABC的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高中入学新生的身高情况,从高一年级学生中按分层抽样共抽取了50名学生的身高数据,分组统计后得到了这50名学生身高的频数分布表:

(Ⅰ)在答题卡上作出这50名学生身高的频率分布直方图;
(Ⅱ)估计这50名学生身高的方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从身高在![]() 这6名学生中随机抽取3名,求至少抽到1名女生的概率.
这6名学生中随机抽取3名,求至少抽到1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com