
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点.
中点.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求证:![]() .
.
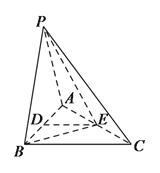
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1) ∵![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,∴
中点,∴![]() ,根据线面平行的判定定理即可证明;(2)先分别证明
,根据线面平行的判定定理即可证明;(2)先分别证明![]() 和
和![]() ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得![]() 平面
平面![]() ,进而可得
,进而可得![]() .
.
试题解析:
证明:(Ⅰ)∵![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,
中点,
∴![]() .
.
∵![]() 平面
平面![]() ,平面
,平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)连接![]() ,
,
∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
由∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
点睛: 直线与平面平行的定义:如果直线![]() 与平面
与平面![]() 没有公共点,则直线
没有公共点,则直线![]() 与平面
与平面![]() 平行,记作
平行,记作![]() ;直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线互相平行,则该直线与此平面平行; 判定直线和平面垂直的方法:①定义法.②利用判定定理:一条直线和一个平面内的两条相交直线都垂直,则该直线和此平面垂直.③推论:如果在两条平行直线中,有一条垂直于一个平面,那么另一条直线也垂直于这个平面.
;直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线互相平行,则该直线与此平面平行; 判定直线和平面垂直的方法:①定义法.②利用判定定理:一条直线和一个平面内的两条相交直线都垂直,则该直线和此平面垂直.③推论:如果在两条平行直线中,有一条垂直于一个平面,那么另一条直线也垂直于这个平面.


科目:高中数学 来源: 题型:
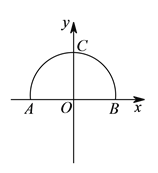
【题目】如图是一段圆锥曲线,曲线与两个坐标轴的交点分别是![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)若该曲线表示一个椭圆,设直线![]() 过点
过点![]() 且斜率是
且斜率是![]() ,求直线
,求直线![]() 与这个椭圆的公共点的坐标.
与这个椭圆的公共点的坐标.
(Ⅱ)若该曲线表示一段抛物线,求该抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站针对2015年中国好声音歌手A,B,C三人进行网上投票,结果如下
观众年龄 | 支持A | 支持B | 支持C |
20岁以下 | 100 | 200 | 600 |
20岁以上(含20岁) | 100 | 100 | 400 |
(1)在所有参与该活动的人中,用分层抽样的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分层抽样的方法抽取5人作为一个总体,从这5人中任意选取2人,求恰有1人在20岁以下的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内有向量 ![]() =(1,7),
=(1,7), ![]() =(5,1),
=(5,1), ![]() =(2,1),点X为直线OP上的一个动点.
=(2,1),点X为直线OP上的一个动点.
(1)当 ![]()
![]() 取最小值时,求
取最小值时,求 ![]() 的坐标;
的坐标;
(2)当点X满足(1)的条件和结论时,求cos∠AXB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示. 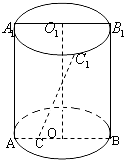
(1)求圆柱体的侧面积S侧的值;
(2)若C1是半圆弧 ![]() 的中点,点C在半径OA上,且OC=
的中点,点C在半径OA上,且OC= ![]() OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和直线
和直线![]() ,直线
,直线![]() ,
, ![]() 都经过圆
都经过圆![]() 外定点
外定点![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 交于
交于![]() 点,且线段
点,且线段![]() 的中点为
的中点为![]() ,
,
求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com