
【题目】在△ABC中,已知![]() =3
=3![]() .
.
(1)求证:tan B=3tan A;
(2)若cos C=![]() ,求A的值.
,求A的值.
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知内角 ![]() ,边
,边 ![]() .设内角B=x,△ABC的面积为y.
.设内角B=x,△ABC的面积为y.
(1)求函数y=f(x)的解析式和定义域;
(2)当角B为何值时,△ABC的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇). 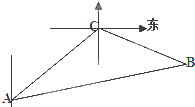
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是半圆
是半圆![]() 的直径,
的直径, ![]() 是半圆
是半圆![]() 上除
上除![]() 、
、![]() 外的一个动点,
外的一个动点, ![]() 垂直于半圆
垂直于半圆![]() 所在的平面,
所在的平面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
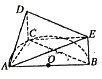
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛B的正南A处,AB=10千米.甲船以每小时4千米的速度向北航行,同时,乙船自B出发以每小时6千米的速度向北偏东60°的方向驶去.当甲船在A,B之间,且甲、乙两船相距最近时,它们所航行的时间是( )

A. ![]() 分钟 B.
分钟 B. ![]() 小时 C. 21.5分钟 D. 2.15分钟
小时 C. 21.5分钟 D. 2.15分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]()
![]() ,说明满足条件的点
,说明满足条件的点![]() 的轨迹,并求
的轨迹,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
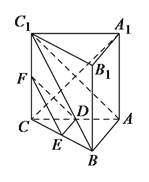
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)若线段![]() 上的点
上的点![]() 满足平面
满足平面![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并说明理由.
的位置,并说明理由.
(Ⅲ)证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com