
分析 先利用已知f(x)是定义在R上的偶函数求出在区间[0,2]上的解析式,再利用周期性f(x)=f(x+4)求出函数f(x)在区间[2,4]上的解析式,然后在画出图象,进而求出a的取值范围
解答 解:x∈[0,2],f(x)=2x-1,
∵对任意x∈R,都有f(x)=f(x+4),
∴当x∈[2,4]时,(x-4)∈[-2,0],
∵f(x)是定义在R上的偶函数,
∴f(x)=f(x-4)=2x-4-1;
当x∈[4,6]时,(x-4)∈[0,2],∴f(x)=f(x-4)=2x-4-1.
∵若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有三个不同的实数根,
∴函数y=f(x)与函数y=loga(x+2)在区间(-2,6]上恰有三个交点,
故函数f(x)在区间(-2,6]上的图象如下图所示: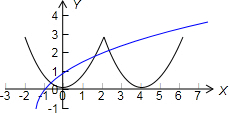
通过画图可知:
恰有三个交点的条件是$\left\{\begin{array}{l}{{log}_{a}^{(6+2)}>3}\\{{log}_{a}^{2+2}<3}\end{array}\right.$,解得 ${2}^{\frac{2}{3}}$<a<2,
即 $\root{3}{4}$<a<2,因此所求的a的取值范围为($\root{3}{4}$,2).
故答案为:($\root{3}{4}$,2).
点评 本题综合考查了函数的奇偶性、周期性、函数的交点及方程的根,熟练掌握函数的性质及数形结合是解决问题的关键.


科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(文)试卷(解析版) 题型:解答题
已知函数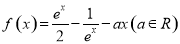 .
.
(1)当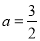 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数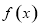 在
在 上为单调函数,求实数
上为单调函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(tanα)>f(tanβ) | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在与边AB垂直的直线上 | B. | 在∠A的平分线所在直线上 | ||
| C. | 在边AB的中线所在直线上 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com