
已知函数f (x) = ln(ex + a)(a为常数)是实数集R上的奇函数,函数g (x) =
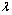 f
(x) + sinx是区间[–1,1]上的减函数.
f
(x) + sinx是区间[–1,1]上的减函数.
(1)求a的值;
(2)若g (x)≤t2 +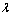 t
+ 1在x∈[–1,1]上恒成立,求t的取值范围;
t
+ 1在x∈[–1,1]上恒成立,求t的取值范围;
(3)讨论关于x的方程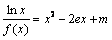 的根的个数.
的根的个数.
【解析】(1)由于f (x) 是R上的奇函数,f (0) = 0,故a = 0.……………………3分
(2)∵g (x)在[–1,1]上单调递减,∴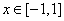 时
时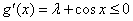 恒成立
恒成立
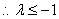 ,
,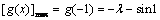
∴只要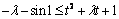
∴(t + 1)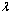 +
t2 + sin1 + 1≥0(其中
+
t2 + sin1 + 1≥0(其中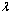 ≤–1)恒成立.……………………5分
≤–1)恒成立.……………………5分
令
则
∴t≤–1.………………………………………………………………………………8分
(3)由(1)知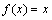 .∴方程为
.∴方程为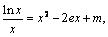
令f1(x) =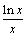 ,f2(x)
= x2 – 2ex + m,
,f2(x)
= x2 – 2ex + m,
∵
当x∈(0,e)时,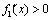 ,∴
,∴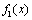 在(0,e]上为增函数;
在(0,e]上为增函数;
当x∈(e,+∞)时, ,∴
,∴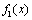 在(e,+∞)上为减函数;
在(e,+∞)上为减函数;
当x = e时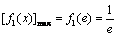 .
.
而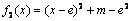
∴当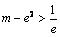 时,即
时,即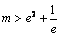 时方程无解.
时方程无解.
当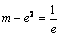 时,即
时,即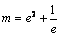 时方程有一解.
时方程有一解.
当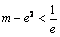 时,即
时,即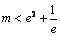 时方程有二解.………………………………………13分
时方程有二解.………………………………………13分


科目:高中数学 来源: 题型:
|
| 1 |
| π |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-1 | x+a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com