
已知函数 在
在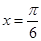 处有极值,则函数
处有极值,则函数 的图象可能是( )
的图象可能是( )




A. B. C. D.
A
【解析】
试题分析:因为,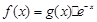 ,令
,令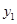 =
=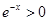 是减函数,
是减函数,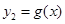 。
。
图象B中,在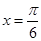 处,
处,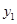 和
和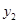 绝对值为正且都处于减小过程中,两都相乘后的函数f(x)为正且是处于减小过程,不可能存在极值;
绝对值为正且都处于减小过程中,两都相乘后的函数f(x)为正且是处于减小过程,不可能存在极值;
图象C中,在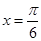 处,
处,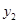 为负且绝对值持续减小,而
为负且绝对值持续减小,而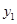 也是持续减小,相乘后f(x)绝对值仍为负且继续减小,不存在极值;
也是持续减小,相乘后f(x)绝对值仍为负且继续减小,不存在极值;
图象D中,在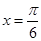 处,
处,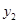 由负变正而
由负变正而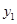 持续减小,f(x)将由负变正,虽不能肯定之后函数走势,但该处不可能是极值点;
持续减小,f(x)将由负变正,虽不能肯定之后函数走势,但该处不可能是极值点;
图象A所示情形,在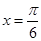 处,
处,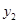 为负但绝对值继续增加,而
为负但绝对值继续增加,而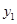 是持续减小,两者相乘后f(x)保持为负但绝对值可能不会再增大,有可能存在极值。
是持续减小,两者相乘后f(x)保持为负但绝对值可能不会再增大,有可能存在极值。
考点:本题主要考查函数极值存在的条件,函数的图象。
点评:中档题,结合函数图象,定性估计函数极值的情况,具有“猜测”成分。


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源:2012-2013学年河北省高三第三次模拟考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数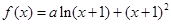 在
在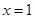 处有极值.
处有极值.
(Ⅰ)求实数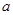 值;
值;
(Ⅱ)求函数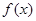 的单调区间;
的单调区间;
(Ⅲ)试问是否存在实数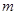 ,使得不等式
,使得不等式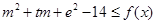 对任意
对任意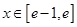 及
及
恒成立?若存在,求出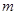 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.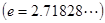
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com