
如图,四棱锥P-ABCD的底面是矩形,侧面PAD丄底面ABCD,. .
.
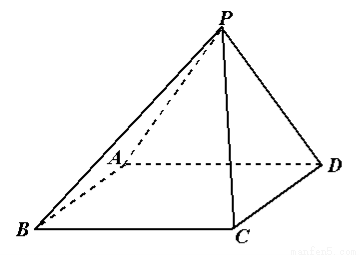
(1)求证:平面PAB丄平面PCD
(2)如果AB=BC=2,PB=PC=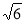 求四棱锥P-ABCD的体积.
求四棱锥P-ABCD的体积.
(1) 见解析 (2)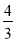
【解析】
试题分析:(1)欲证平面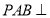 平面
平面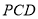 ,只需证其中的一个平面经过另一平面的一条垂线即可,考虑到题设中所给的矩形以及面面垂直关系,易证:
,只需证其中的一个平面经过另一平面的一条垂线即可,考虑到题设中所给的矩形以及面面垂直关系,易证: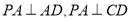 ,从而
,从而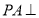 平面
平面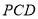 ;
;
(2)作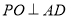 ,垂足为
,垂足为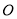 ,连结
,连结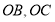 ;可证
;可证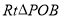 ≌
≌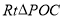
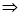
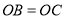
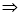
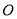 是
是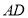 的中点,
的中点,
从而求得四棱锥的高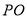 ,进一步求得四棱锥
,进一步求得四棱锥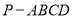 的体积.
的体积.
试题解析:(Ⅰ)因为四棱锥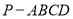 的底面是矩形,所以
的底面是矩形,所以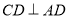 ,
,
又侧面 底面
底面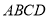 ,所以
,所以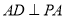 .
.
又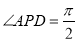 ,即
,即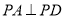 ,而
,而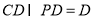 ,所以
,所以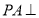 平面
平面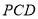 .
.
因为PA?平面PAB,所以平面PAB⊥平面PCD. 4分
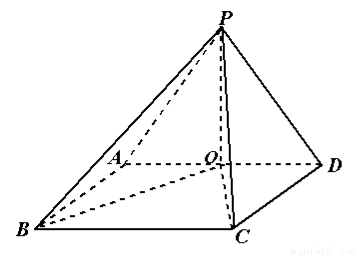
(Ⅱ)如图,作PO⊥AD,垂足为O,则PO⊥平面ABCD.
连结OB,OC,则PO⊥OB,PO⊥OC.
因为PB=PC,所以Rt△POB≌Rt△POC,所以OB=OC.
依题意,ABCD是边长为2的正方形,由此知O是AD的中点. 7分
在Rt△OAB中,AB=2,OA=1,OB=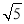 .
.
在Rt△OAB中,PB=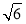 ,OB=
,OB=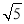 ,PO=1. 10分
,PO=1. 10分
故四棱锥P-ABCD的体积V=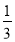 AB2·PO=
AB2·PO=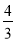 .
.
考点:1、平面与平面垂直的判定与性质;2、棱锥的体积.


 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:2016届河北省高一下学期第一次月考理科数学试卷(解析版) 题型:解答题
已知正项数列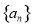 的前
的前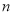 项和为
项和为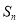 ,且
,且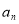 和
和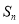 满足:
满足: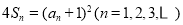 .
.
(1)求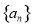 的通项公式;
的通项公式;
(2)设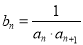 ,求
,求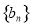 的前
的前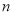 项和
项和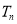 ;
;
(3)在(2)的条件下,对任意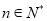 ,
,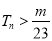 都成立,求整数
都成立,求整数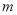 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2016届河北省衡水市高一下学期期末考试数学试卷(解析版) 题型:选择题
.已知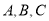 为平面上不共线的三点,若向量
为平面上不共线的三点,若向量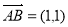 ,
,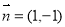 ,且
,且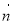 ·
·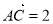 ,则
,则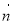 ·
· 等于( ).
等于( ).
A.-2 B.0 C.2 D.2或-2
查看答案和解析>>
科目:高中数学 来源:2016届河北省高一下学期期中考试理科数学试卷(解析版) 题型:填空题
若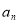 =2
=2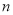 2+λ
2+λ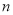 +3(其中λ为实常数),
+3(其中λ为实常数),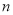 ∈N*,且数列{
∈N*,且数列{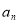 }为单调递增数列,则实数λ的取值范围为________.
}为单调递增数列,则实数λ的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com