
【题目】如图,关于正方体![]() ,有下列四个命题:
,有下列四个命题:
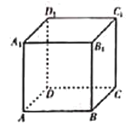
①![]() 与平面
与平面![]() 所成角为45°;
所成角为45°;
②三棱锥![]() 与三棱锥
与三棱锥![]() 的体积比为
的体积比为![]() ;
;
③存在唯一平面![]() .使
.使![]() 平面
平面![]() 且
且![]() 截此正方体所得截面为正六边形;
截此正方体所得截面为正六边形;
④过![]() 作平面
作平面![]() ,使得棱
,使得棱![]() 、
、![]() ,
,![]() 在平面
在平面![]() 上的正投影的长度相等.则这样的平面
上的正投影的长度相等.则这样的平面![]() 有且仅有一个.
有且仅有一个.
上述四个命题中,正确命题的序号为________.
【答案】①②③.
【解析】
根据线面角的求解方法,三棱锥体积计算公式,正方体截面的性质,以及投影的相关知识,对选项进行逐一分析即可.
对①:过![]() 作
作![]() 垂直于
垂直于![]() ,垂足为
,垂足为![]() ,如下图所示:
,如下图所示:
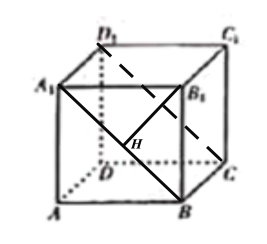
因为![]() 是正方体,
是正方体,
容易知![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,故可得
,故可得![]() ,
,
又因为![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() 即为所求线面角.
即为所求线面角.
容易知![]() 为等腰直角三角形,故
为等腰直角三角形,故![]() .
.
即![]() 与平面
与平面![]() 所成角为45°.故①正确;
所成角为45°.故①正确;
对②:设正方体棱长为1,
故可得![]() ;
;
而棱锥![]() 的体积可以理解为
的体积可以理解为
正方体的体积减去4个体积都和![]() 相等的三棱锥的体积,
相等的三棱锥的体积,
故![]() .
.
故棱锥![]() 与三棱锥
与三棱锥![]() 的体积比为
的体积比为![]() ,则②正确;
,则②正确;
对③:根据正方体截面的性质,当截面为六边形时,
当且仅当![]() 为各点所在棱的中点时,截面为正六边形,如下图所示:
为各点所在棱的中点时,截面为正六边形,如下图所示:
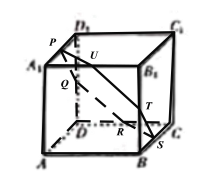
其它情况下,无法保证截面六边形的棱长都相等,
故存在唯一平面![]() .使
.使![]() 平面
平面![]() 且
且![]() 截此正方体所得截面为正六边形,
截此正方体所得截面为正六边形,
则③正确;
对④:若棱![]() 在平面
在平面![]() 的同侧,则
的同侧,则![]() 为过点
为过点![]() 且与平面
且与平面![]() 平行的平面;
平行的平面;
若棱![]() 中有一条棱与另外两条棱分别在平面
中有一条棱与另外两条棱分别在平面![]() 的异侧,则这样的平面有3个;
的异侧,则这样的平面有3个;
故满足题意的平面![]() 有4个.
有4个.
故④错误.
综上所述:正确的有①②③.
故答案为:①②③.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为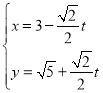 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为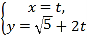 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】造纸术是我国古代四大发明之一.纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、…、
、…、![]() ;
;![]() 、
、![]() 、…、
、…、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,其中
系列,其中![]() 系列的幅面规格为:①
系列的幅面规格为:①![]() 规格的纸张的幅宽(以
规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系为
表示)的比例关系为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格.
规格.![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 纸各一张.若
纸各一张.若![]() 纸的面积为
纸的面积为![]() ,则这9张纸的面积之和等于______
,则这9张纸的面积之和等于______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来就一直使用的纪年方法.其中干支是天干:甲、乙、丙、丁、戊、已、庚、辛、壬、癸十个符号;地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个符号.把干支顺序相配正好六十为一周,周而复始,循环记录,即甲子、乙丑、丙寅、…….2020年是“庚子年”,则我国建国一百周年(2049年)是_______年.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com