
���� ��1����$x=2\sqrt{3}cos\frac{��}{6}$=3��y=2$\sqrt{3}sin\frac{��}{6}$=$\sqrt{3}$���������P��ֱ�����꣬��$\left\{\begin{array}{l}x=2cos��\\ y=-\sqrt{3}+2sin��\end{array}\right.$����ȥ�գ����������C��ֱ�����귽�̣�
��2�����ֱ��l����ͨ����Ϊ4x+3y+1=0����$Q��2cos�գ�-\sqrt{3}+2sin�գ�$����$M��\frac{3}{2}+cos�գ�sin�գ�$�����õ㵽ֱ��l�ľ��빫ʽ�������M��ֱ��l����С���룮
��� �⣺��1����P��ļ�����Ϊ��2$\sqrt{3}$��$\frac{��}{6}$����
$x=2\sqrt{3}cos\frac{��}{6}$=3��y=2$\sqrt{3}sin\frac{��}{6}$=$\sqrt{3}$��
���P��ֱ������Ϊ$��3��\sqrt{3}��$��
��$\left\{\begin{array}{l}x=2cos��\\ y=-\sqrt{3}+2sin��\end{array}\right.$����ȥ�յã�${x^2}+{��y+\sqrt{3}��^2}=4$��
������C��ֱ�����귽��Ϊ${x^2}+{��y+\sqrt{3}��^2}=4$������5�֣�
��2������C�IJ�������Ϊ$\left\{\begin{array}{l}x=2cos��\\ y=-\sqrt{3}+2sin��\end{array}\right.$����Ϊ��������
��ֱ��l�ļ����귽��Ϊ4��cos��+3��sin��+1=0��
��ֱ��l����ͨ����Ϊ4x+3y+1=0��
��$Q��2cos�գ�-\sqrt{3}+2sin�գ�$����$M��\frac{3}{2}+cos�գ�sin�գ�$��
���M��ֱ��l�ľ���Ϊ$d=\frac{|4cos��+3sin��+7|}{5}=\frac{|5sin����+����+7|}{5}��\frac{2}{5}$��
���M��ֱ��l����С����Ϊ$\frac{2}{5}$������10�֣�
���� ���⿼����ֱ�����꼰���ߵ���ͨ���̵���ʾ�������߶����е㵽ֱ�߾������Сֵ�������е��⣬����ʱҪ�������⣬ע���е����깫ʽ���㵽ֱ�ߵľ��빫ʽ�ĺ������ã�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ | B�� | ��Ҫ����� | ||
| C�� | ��Ҫ | D�� | �Ȳ�����ֲ���Ҫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ∅ | B�� | {1��3��5} | C�� | {2��4} | D�� | {1��2��3��4��5} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{8}$ | D�� | $\frac{1}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
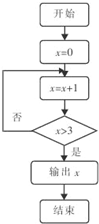
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com