
【题目】![]() .
.
(1)若 ![]() 时,
时, ![]() ,求cos4x的值;
,求cos4x的值;
(2)将 ![]() 的图象向左移
的图象向左移 ![]() ,再将各点横坐标伸长为原来的2倍,纵坐标不变,得y=g(x),若关于g(x)+m=0在区间
,再将各点横坐标伸长为原来的2倍,纵坐标不变,得y=g(x),若关于g(x)+m=0在区间 ![]() 上的有且只有一个实数解,求m的范围.
上的有且只有一个实数解,求m的范围.
【答案】
(1)解: ![]() =(
=( ![]() sin2x,cos2x),
sin2x,cos2x), ![]() =(cos2x,﹣cos2x),
=(cos2x,﹣cos2x),
∴f(x)= ![]()
![]() +
+ ![]()
= ![]() sin2xcos2x﹣cos22x+
sin2xcos2x﹣cos22x+ ![]()
= ![]() sin4x﹣
sin4x﹣ ![]() cos4x﹣
cos4x﹣ ![]() +
+ ![]()
=﹣cos(4x+ ![]() )=﹣
)=﹣ ![]() ,
,
∴cos(4x+ ![]() )=
)= ![]() ;
;
又 ![]() 时,4x+
时,4x+ ![]() ∈(
∈( ![]() ,2π),
,2π),
∴sin(4x+ ![]() )=﹣
)=﹣ 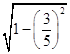 =﹣
=﹣ ![]() ,
,
∴cos4x=cos[(4x+ ![]() )﹣
)﹣ ![]() ]
]
=cos(4x+ ![]() )cos
)cos ![]() +sin(4x+
+sin(4x+ ![]() )sin
)sin ![]()
= ![]() ×
× ![]() +(﹣
+(﹣ ![]() )×
)× ![]()
= ![]() ;
;
(2)解:由(1)知,f(x)= ![]() sin4x﹣
sin4x﹣ ![]() cos4x=sin(4x﹣
cos4x=sin(4x﹣ ![]() ),
),
将f(x)的图象向左平移 ![]() 个单位,得y=sin[4(x+
个单位,得y=sin[4(x+ ![]() )﹣
)﹣ ![]() ]=sin(4x+
]=sin(4x+ ![]() )的图象;
)的图象;
再将y各点横坐标伸长为原来的2倍,纵坐标不变,得y=sin(2x+ ![]() )的图象;
)的图象;
则y=g(x)=sin(2x+ ![]() );
);
当x∈ ![]() 时,2x+
时,2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
画出函数g(x)的图象,如图所示;
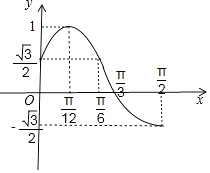
则g(x)+m=0在区间 ![]() 上的有且只有一个实数解时,
上的有且只有一个实数解时,
应满足﹣ ![]() ≤﹣m<
≤﹣m< ![]() 或﹣m=1;
或﹣m=1;
即﹣ ![]() <m≤
<m≤ ![]() ,或m=﹣1.
,或m=﹣1.
【解析】(1)由题意,根据平面向量的数量积运算求出cos(4x+ ![]() )的值,再利用三角恒等变换求出cos4x的值;(2)由(1)知f(x)的解析式,利用图象平移和变换得出g(x)的解析式,画出函数g(x)的图象,结合图象求出m的取值范围.
)的值,再利用三角恒等变换求出cos4x的值;(2)由(1)知f(x)的解析式,利用图象平移和变换得出g(x)的解析式,画出函数g(x)的图象,结合图象求出m的取值范围.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,给出的是计算 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() 的值的程序框图,其中判断框内可填入的是( )
的值的程序框图,其中判断框内可填入的是( ) 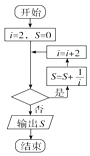
A.i≤2 021?
B.i≤2 019?
C.i≤2 017?
D.i≤2 015?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求函数f(x)的最小正周期和单调增区间;
(2)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知(a2+b2)sin(A﹣B)=(a2﹣b2)sin(A+B),则△ABC的形状( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(cosα,sinα),设
=(cosα,sinα),设 ![]() =
= ![]() +t
+t ![]() (t为实数).
(t为实数).
(1)若 ![]() ,求当|
,求当| ![]() |取最小值时实数t的值;
|取最小值时实数t的值;
(2)若 ![]() ⊥
⊥ ![]() ,问:是否存在实数t,使得向量
,问:是否存在实数t,使得向量 ![]() ﹣
﹣ ![]() 和向量
和向量 ![]() 的夹角为
的夹角为 ![]() ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙M:(x+1)2+y2= ![]() 的圆心为M,⊙N:(x﹣1)2+y2=
的圆心为M,⊙N:(x﹣1)2+y2= ![]() 的圆心为N,一动圆M内切,与圆N外切. (Ⅰ)求动圆圆心P的轨迹方程;
的圆心为N,一动圆M内切,与圆N外切. (Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)设A,B分别为曲线P与x轴的左右两个交点,过点(1,0)的直线l与曲线P交于C,D两点.若 ![]() =12,求直线l的方程.
=12,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为1,圆心角为 ![]() 的圆弧
的圆弧 ![]() 上有一点C.
上有一点C. 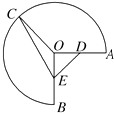
(1)若C为圆弧AB的中点,点D在线段OA上运动,求| ![]() |的最小值;
|的最小值;
(2)若D,E分别为线段OA,OB的中点,当C在圆弧 ![]() 上运动时,求
上运动时,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com