
科目:高中数学 来源: 题型:
已知函数f(x)=x3+ax2+bx. 若y=f(x)的导数f′(x)对x∈[-1,1]都有f′(x)≤2,则 的范围 ( )
的范围 ( )
A.(-2,1] B.(-∞,-2)∪[1,+∞). C.( , 1]. D. [-2,
, 1]. D. [-2, ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角 的始边为射线
的始边为射线 ,终边为射线
,终边为射线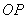 ,过点
,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为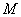 ,将点
,将点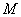 到直线
到直线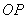 的距离表示为
的距离表示为 的函数
的函数 ,则
,则 =
= 在[0,
在[0,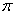 ]上的图像大致为
]上的图像大致为
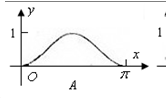
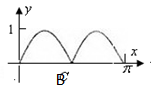

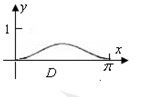
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线 :
: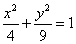 ,直线
,直线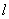 :
: (
( 为参数).
为参数).
(Ⅰ)写出曲线 的参数方程,直线
的参数方程,直线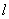 的普通方程;
的普通方程;
(Ⅱ)过曲线 上任一点
上任一点 作与
作与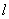 夹角为
夹角为 的直线,交
的直线,交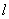 于点
于点 ,求
,求 的最大值与最小值.
的最大值与最小值.
24. (本小题满分10分)选修4—5:不等式选讲
若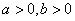 ,且
,且 .
.
(Ⅰ) 求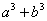 的最小值;
的最小值;
(Ⅱ)是否存在 ,使得
,使得 ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,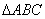 是圆的内接三角行,
是圆的内接三角行,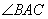 的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分
的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分 ;②
;②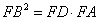 ;③
;③ ;④
;④ .则所有正确结论的序号是( )
.则所有正确结论的序号是( )
A.①② B.③④ C.①②③ D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,四棱锥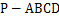 的底面
的底面 是平行四边形,
是平行四边形, ,
, ,
,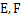 分别是棱
分别是棱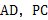 的中点.
的中点.
证明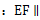 平面
平面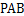 ;
;
若二面角P-AD-B为 ,
,
证明:平面PBC⊥平面ABCD
求直线EF与平面PBC所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com