练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．作出函数y=log${\;}_{\frac{1}{2}}$|x+2|的图象．

    分析 对x的取值进行讨论，去掉绝对值符号，转化成对数函数的形式，再结合对数函数的图象与性质，即可画出图象．

    解答 解：化简函数y=log${\;}_{\frac{1}{2}}$|x+2|=$\left\{\begin{array}{l}{{log}_{\frac{1}{2}}（x+2），x＞-2}\\{{log}_{\frac{1}{2}}（-x-2），x＜-2}\end{array}\right.$，
    利用列表、描点、连线的方法，
    即可作出函数y=log${\;}_{\frac{1}{2}}$|x+2|的图象，如图所示；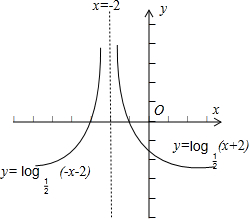

    点评 本题考查了对数函数的图象与性质的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．圆心在抛物线y2=2x（y≥0）上，经过点（2，0）且面积最小的圆为⊙C，直线y=kx+2与⊙C相交于A，B两点，当弦长|AB|取得最小值时k=$\frac{2+\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机抽调了50人，他们年龄的频数分布及支持“生育二胎”人数如下表：
    年龄[5，15）[15，25）[25，35）[35，45）[45，55）[55，65）
    频数510151055
    支持“生育二胎”4512821
    （Ⅰ）由以上统计数据填下面2×2列联表；
    年龄不低于45岁的人年龄低于45岁的人合计
    支持“生育二胎”a=3c=2932
    不支持“生育二胎”b=7d=1118
    合计1040n=50
    （Ⅱ）判断是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异．
    P（K2≥k）0.0500.0100.001
    k3.8416.63510.828
    附表：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

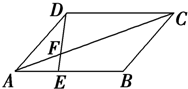
    20．如图，平行四边形ABCD中，AE：EB=1：2，若△AEF的面积等于2cm2，则△CDF的面积等于（　　） 
    A．16 cm2B．18 cm2C．20 cm2D．22 cm2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知f（x）=|x+2|-|x-1|
    （1）请画出f（x）的图象；
    （2）函数f（x）的最大值是3，最小值是-3；
    （3）函数f（x）的值域是[-3，3]；
    （4）f（x）＜4的解集是R；
    （5）若不等式f（x）＞a对所有的x都成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知sinα-cosα=$\frac{1}{5}$，且0＜α＜π，
    （1）求sin（2α-$\frac{π}{4}$）的值；
    （2）求$\frac{sin2α+2si{n}^{2}α}{1-tanα}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知双曲线的一个顶点为（2，0），且渐近线的方程为y=±x，那么该双曲线的标准方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}=1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．指出下列命题的形式及构成它的命题．
    （1）24既是8的倍数，又是6的倍数；
    （2）菱形是圆的内接四边形或是圆的外切四边形；
    （3）矩形不是平行四边形．

    查看答案和解析>>

    科目：高中数学 来源：2017届甘肃会宁县一中高三上学期9月月考数学（理）试卷（解析版） 题型：解答题

    选修4—5：不等式选讲

    已知函数f（x）＝|2x－a|＋a.

    （1）若不等式f（x）≤6的解集为{x|－2≤x≤3}，求实数a的值；

    （2）在（1）的条件下，若存在实数n使f（n）≤m－f（－n）成立，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案