Question

【题目】已知函数f（x）=lnx+x2﹣ax（a∈R）
（1）a=3时，求函数f（x）的单调区间；
（2）若f（x）≤2x2恒成立，求实数a的取值范围；
（3）求证；lnn＞ + +1 +…+ （n∈N+）且n≥2．

Answer 1

【答案】
（1）解：a=3时，f（x）=lnx+x2﹣3x，（x＞0），

f′（x）= +2x﹣3= ，

△=32﹣8=1＞0，由f′（x）=0，解得x1= ，x2=1，

当x∈（0， ）∪（1，+∞）时，f′（x）＞0，当x∈（ ）时，f′（x）＜0，

则函数f（x）在（0， ），（1，+∞）上单调递增，在（ ，1）上单调递减

（2）解：f（x）≤2x2，化为：lnx﹣x2﹣ax≤0，

∴a≥ ﹣x，令g（x）= ，

g′（x）= ，

令h（x）=1﹣lnx﹣x2，可知：函数h（x）在（0，+∞）上单调递减．

而h（1）=0=g′（1）．

∴x＞1时，g′（x）＜0，函数g（x）单调递减；

0＜x＜1时，g′（x）＞0，函数g（x）单调递增．

∴函数g（x）在x=1时取得极大值即最大值，g（1）=﹣1．

∴实数a的取值范围是a≥﹣1

（3）证明：令t（x）=lnx﹣ ，

则t′（x）= ＞0，

∴t（x）在（0，+∞）上单调递增，

当x＞1时，t（x）＞t（1），即lnx﹣ ＞0，∴lnx＞ ，

令x=1+ ，则ln（1+ ）＞ ，

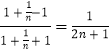故ln（1+1）＞ ，ln（1+ ）＞ ，…，ln（1+ ）＞ ．

累加得：ln（n+1）＞ ，

取n=n﹣1，得lnn＞ （n≥2）

【解析】（1）把a=3代入函数解析式，求导后求得导函数零点，由导函数零点对定义域分段，求出各区间段内导函数的符号，从而求得原函数的单调区间；（2）把f（x）≤2x2化为：lnx﹣x2﹣ax≤0，得到a≥ ﹣x，令g（x）= ，利用导数求其最大值可得实数a的取值范围；（3）令t（x）=lnx﹣ ，由导数可得t（x）在（0，+∞）上单调递增，得到x＞1时，lnx＞ ，令x=1+ ，可得ln（1+ 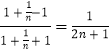）＞ ，累加可得ln（n+1）＞ ，取n=n﹣1得答案．
【考点精析】根据题目的已知条件，利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值．