
����Ŀ������ѧ���ۺ���������ij��ά�ȵIJ����У��֡����㡢�ϸ��д��Ľ��������ȼ�����ѧ��������ijУ�߶��꼶������500�ˣ�Ů��400�ˣ�Ϊ���˽��Ա��ά�Ȳ��������Ӱ�죬���÷ֲ���������Ӹ߶��꼶��ȡ��45��ѧ���IJ��������������Ƶ��ͳ�Ʊ������ ��һ�������������ͳ��
�ȼ� | ���� | �ϸ� | �д��Ľ� |
Ƶ�� | 15 | x | 5 |
������Ů���������ͳ��
�ȼ� | ���� | �ϸ� | �д��Ľ� |
Ƶ�� | 15 | 3 | y |
�ο����ݣ�
P��K2��k0�� | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���ο���ʽ�� ![]() ������n=a+b+c+d����
������n=a+b+c+d����
��1������x��y��ֵ��
��2���ɱ�һ������ͳ���������2��2�����������ж��Ƿ���90%�İ�����Ϊ����������������Ա��йء���
���� | Ů�� | �ܼ� | |
���� | |||
������ | |||
�ܼ� |
���𰸡�
��1���⣺��Ӹ�һ�꼶�����г��m�ˣ�
�� ![]() �����m=25��
�����m=25��
��x=25��20=5��y=20��18=2
��2���⣺2��2����������
���� | Ů�� | �ܼ� | |
���� | 15 | 15 | 30 |
������ | 10 | 5 | 15 |
�ܼ� | 25 | 20 | 45 |
�� ![]() ��
��
��û��90%�İ�����Ϊ����������������Ա��йء�
����������1�����ݷֲ�����Ķ����������ռ�ı����г����̣����m��ֵ�������������x��y��ֵ����2���ɣ�1���г����������������ݺ�ʽ���K2�Ĺ۲�ֵ���ɱ���Ͷ����Լ��鼴�ɵõ��𰸣�


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
(1)����![]() �ĵ������䣻
�ĵ������䣻
(2)������![]() �IJ���ʽ
�IJ���ʽ![]() �������������
�������������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪2����Ʒ��3����Ʒ�����һ������Ҫͨ����⽫�����֣�ÿ��������һ����Ʒ�����Żأ�ֱ������2����Ʒ������3����Ʒʱ������.
���������һ�μ������Ǵ�Ʒ�ҵڶ��μ���������Ʒ�ĸ��ʣ�
��������֪ÿ���һ����Ʒ��Ҫ����100Ԫ����![]() ��ʾֱ������2����Ʒ������3����Ʒʱ����Ҫ�ļ����ã���λ��Ԫ������
��ʾֱ������2����Ʒ������3����Ʒʱ����Ҫ�ļ����ã���λ��Ԫ������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������⣺ �ٺ��� ![]() ��һ���Գ�����x=
��һ���Գ�����x= ![]() ��
��
�ں���y=tanx��ͼ����ڵ㣨 ![]() ��0���Գƣ�
��0���Գƣ�
�����Һ����ڵ�һ����Ϊ��������
���� ![]() ����x1��x2=k������k��Z��
����x1��x2=k������k��Z��
�ݺ���f��x��=sinx+2|sinx|��x��[0��2��]��ͼ����ֱ��y=k���ҽ���������ͬ�Ľ��㣬��k��ȡֵ��ΧΪ��1��3����
���������������ȷ��������д������ȷ�������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ��x2+x+1��nչ������n=1��2��3����ʱ���õ�������ʾ��չ��ʽ����ͼ��ʾ�Ĺ�����������Σ� ��x2+x+1��0=1
��x2+x+1��1=x2+x+1
��x2+x+1��2=x4+2x3+3x2+2x+1
��x2+x+1��3=x6+3x5+6x4+7x3+6x2+3x+1
�۲����ʽϵ��֮��Ĺ�ϵ�����Է�����������ι�����ͼ��ʾ�Ĺ�����������Σ��乹�췽������0��Ϊ1�����¸���ÿ��������ͷ��������������3��������3���ģ�ȱ�ٵ�����Ϊ0��֮�ͣ���k�й���2k+1���������ڣ�a+x����x2+x+1��4��չ��ʽ�У�x6���ϵ��Ϊ46����ʵ��a��ֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�У�PD![]() ����ABCD��AB//DC��AD
����ABCD��AB//DC��AD![]() DC��AB=AD=1��DC=2��PD=
DC��AB=AD=1��DC=2��PD=![]() ��MΪ��PB���е㣮
��MΪ��PB���е㣮
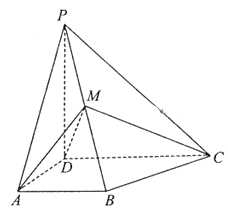
(1)֤����DM![]() ƽ��PBC��
ƽ��PBC��
(2)������A��DM��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ����.
����.
��1����![]() ����
����![]() ʱ���жϺ���
ʱ���жϺ���![]() �Ƿ���ڼ�ֵ�������ڣ������ֵ�㣻�������ڣ�˵�����ɣ�
�Ƿ���ڼ�ֵ�������ڣ������ֵ�㣻�������ڣ�˵�����ɣ�
��2����![]() ���������������
���������������![]() ����
����![]() ʱ����֤��
ʱ����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲO�ķ���Ϊx2+y2=4��P��ԲO�ϵ�һ�����㣬���߶�OP�Ĵ�ֱƽ�������DZ�ƽ������|x|+|y|��a���ǣ���ʵ��a��ȡֵ��Χ�ǣ� ��
A.0��a��2
B.![]()
C.0��a��1
D.a��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lnx+x2��ax��a��R��
��1��a=3ʱ������f��x���ĵ������䣻
��2����f��x����2x2���������ʵ��a��ȡֵ��Χ��
��3����֤��lnn�� ![]() +
+ ![]() +1
+1 ![]() +��+
+��+ ![]() ��n��N+����n��2��
��n��N+����n��2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com