
ЎѕМвДїЎїДП±±іЇК±ґъµДО°ґуКэС§јТЧж•њФЪКэС§ЙПУРН»іц№±ПЧЈ¬ЛыФЪКµјщµД»щґЎЙПМбіцЧж•њФАнЈєЎ°ГЭКЖјИН¬Ј¬Фт»эІ»ИЭТмЎ±.Ждє¬ТеКЗЈєјРФЪБЅёцЖЅРРЖЅГжЦ®јдµДБЅёцјёєОМеЈ¬±»ЖЅРРУЪХвБЅёцЖЅГжµДИОТвЖЅГжЛщЅШЈ¬Из№ыЅШµГµДБЅёцЅШГжµДГж»эЧЬПаµИЈ¬ДЗГґХвБЅёцјёєОМеµДМе»эПаµИЈ¬ИзНјЈ¬јРФЪБЅёцЖЅРРЖЅГжЦ®јдµДБЅёцјёєОМеµДМе»э·Ц±рОЄ![]() Ј¬±»ЖЅРРУЪХвБЅёцЖЅГжµДИОТвЖЅГжЅШµГµДБЅёцЅШГжµДГж»э·Ц±рОЄ
Ј¬±»ЖЅРРУЪХвБЅёцЖЅГжµДИОТвЖЅГжЅШµГµДБЅёцЅШГжµДГж»э·Ц±рОЄ![]() Ј¬ФтЎ°
Ј¬ФтЎ°![]() ЧЬПаµИЎ±КЗЎ°
ЧЬПаµИЎ±КЗЎ°![]() ПаµИЎ±µДЈЁ Ј©
ПаµИЎ±µДЈЁ Ј©
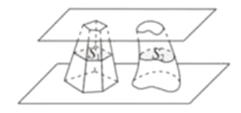
A.ід·ЦІ»±ШТЄМхјюB.±ШТЄІ»ід·ЦМхјю
C.ід·Ц±ШТЄМхјюD.јИІ»ід·ЦТІІ»±ШТЄМхјю
 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪХэИэАвЦщЈЁµЧГжОЄХэИэЅЗРОµДЦ±АвЦщЈ©ABC©ЃA1B1C1ЦРЈ¬ТСЦЄABЈЅAA1ЈЅ2Ј¬µгQОЄBCµДЦРµгЈ®
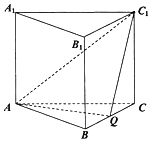
ЈЁ1Ј©ЗуЦ¤ЈєЖЅГжAQC1ЎНЖЅГжB1BCC1Ј»
ЈЁ2Ј©ЗуЦ±ПЯCC1УлЖЅГжAQC1ЛщіЙЅЗµДХэЗРЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬Иф·ЅіМ
Ј¬Иф·ЅіМ![]() УРЛДёцІ»µИКµёщ
УРЛДёцІ»µИКµёщ![]() Ј¬К±Ј¬І»µИКЅ
Ј¬К±Ј¬І»µИКЅ![]() єгіЙБўЈ¬ФтКµКэ
єгіЙБўЈ¬ФтКµКэ![]() µДЧоРЎЦµОЄЈЁЈ©
µДЧоРЎЦµОЄЈЁЈ©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄНЦФІ![]() µДАлРДВКОЄ
µДАлРДВКОЄ![]() Ј¬Ул
Ј¬Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬
Ј¬![]() Ј¬№э
Ј¬№э![]() ЦбЙПТ»µг
ЦбЙПТ»µг![]() Тэ
Тэ![]() ЦбµДґ№ПЯЈ¬Ѕ»НЦФІ
ЦбµДґ№ПЯЈ¬Ѕ»НЦФІ![]() УЪµг
УЪµг![]() Ј¬
Ј¬![]() Ј¬µ±
Ј¬µ±![]() УлНЦФІУТЅ№µгЦШєПК±Ј¬
УлНЦФІУТЅ№µгЦШєПК±Ј¬![]() Ј®
Ј®
ЈЁ1Ј©ЗуНЦФІ![]() µД·ЅіМЈ»
µД·ЅіМЈ»
ЈЁ2Ј©ЙиЦ±ПЯ![]() УлЦ±ПЯ
УлЦ±ПЯ![]() Ѕ»УЪµг
Ѕ»УЪµг![]() Ј¬КЗ·сґжФЪ¶Ёµг
Ј¬КЗ·сґжФЪ¶Ёµг![]() єН
єН![]() Ј¬К№
Ј¬К№![]() ОЄ¶ЁЦµЈ®ИфґжФЪЈ¬Зу
ОЄ¶ЁЦµЈ®ИфґжФЪЈ¬Зу![]() Ўў
Ўў![]() µгµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ®
µгµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛЗмЧЈЦР»ЄИЛГс№ІєН№ъіЙБў![]() ЦЬДкЈ¬ДііµјдДЪѕЩРРЙъІъ±ИИьЈ¬УЙјЧТТБЅЧйДЪёчЛж»ъСЎИЎ
ЦЬДкЈ¬ДііµјдДЪѕЩРРЙъІъ±ИИьЈ¬УЙјЧТТБЅЧйДЪёчЛж»ъСЎИЎ![]() Гыјј№¤Ј¬ФЪµҐО»К±јдЙъІъН¬Т»ЦЦБгјюЈ¬ЖдЙъІъµДєПёсБгјюКэµДѕҐТ¶НјИзПВЈє
Гыјј№¤Ј¬ФЪµҐО»К±јдЙъІъН¬Т»ЦЦБгјюЈ¬ЖдЙъІъµДєПёсБгјюКэµДѕҐТ¶НјИзПВЈє
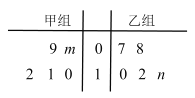
ТСЦЄБЅЧйЛщСЎјј№¤ЙъІъµДєПёсБгјюµДЖЅѕщКэѕщОЄ![]() .
.
ЈЁ1Ј©·Ц±рЗуіц![]() µДЦµЈ»
µДЦµЈ»
ЈЁ2Ј©·Ц±рЗуіцјЧТТБЅЧйјј№¤ФЪµҐО»К±јдДЪјУ№¤µДєПёсБгјюµД·ЅІо![]() єН
єН![]() ,ІўУЙґЛ№АјЖБЅЧйјј№¤µДЙъІъЛ®ЖЅЈ»
,ІўУЙґЛ№АјЖБЅЧйјј№¤µДЙъІъЛ®ЖЅЈ»
ЈЁ3Ј©ИфµҐО»К±јдДЪЙъІъµДєПёсБгјюёцКэІ»РЎУЪЖЅѕщКэµДјј№¤јґОЄЎ°ЙъІъДЬКЦЎ±Ј¬ёщѕЭТФЙПКэѕЭЈ¬ДЬ·сИПОЄёГіµјд50%ТФЙПµДјј№¤¶јКЗЙъІъДЬКЦЈї
(ЧўЈє·ЅІо![]() ,ЖдЦР
,ЖдЦР![]() ОЄКэѕЭ
ОЄКэѕЭ![]() µДЖЅѕщКэ).
µДЖЅѕщКэ).
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈЁ1Ј©ОЄДіКЎ2016ДкїмµЭТµОсБїНіјЖ±нЈ¬НјЈЁ2Ј©ДіКЎ2016ДкїмµЭТµОсКХИлНіјЖ±нЈ¬¶ФНіјЖНјПВБРАнЅвґнОуµДКЗЈЁЈ©
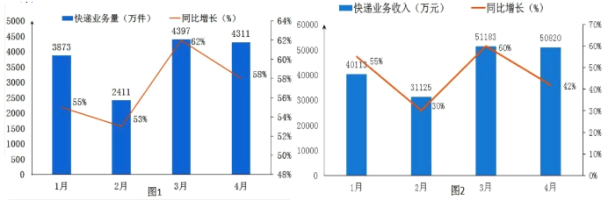
A.2016Дк1Ў«4ФВТµОсБїЧоёЯ3ФВЧоµН2ФВЈ¬ІоЦµЅУЅь2000Нтјю
B.2016Дк1Ў«4ФВТµОсБїН¬±ИФці¤ВКѕщі¬№э50ЈҐЈ¬ФЪ3ФВЧоёЯЈ¬єНґєЅЪХЭ·ьєуНш№єУАґЕзХЗУР№Ш
C.ґУБЅНјЦРїґЈ¬ФцБїУлФці¤ЛЩ¶ИІўІ»НкИ«Т»ЦВЈ¬µ«ТµОсБїУлТµОсµДКХИл±д»ЇёЯ¶ИТ»ЦВ
D.ґУ1Ў«4ФВАґїґЈ¬ТµОсБїУлТµОсКХИлБїУРІЁ¶ЇЈ¬µ«ХыМе±ЈіЦёЯЛЩФці¤
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОЄЧФИ»¶ФКэµДµЧКэЈ®
ОЄЧФИ»¶ФКэµДµЧКэЈ®
ЈЁ1Ј©µ±![]() К±Ј¬ЕР¶П
К±Ј¬ЕР¶П![]() БгµгёцКэІўЗуіцБгµгЈ»
БгµгёцКэІўЗуіцБгµгЈ»
ЈЁ2Ј©ИфєЇКэ![]() ґжФЪБЅёцІ»Н¬µДј«Цµµг
ґжФЪБЅёцІ»Н¬µДј«Цµµг![]() Ј¬
Ј¬![]() Ј¬ЗуКµКэ
Ј¬ЗуКµКэ![]() µДИЎЦµ·¶О§Ј®
µДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪРВёЯїјёДёпЦРЈ¬ґтЖЖБЛОДАн·ЦїЖµДЎ°![]() Ў±ДЈКЅЈ¬І»ЙЩКЎ·ЭІЙУГБЛЎ°
Ў±ДЈКЅЈ¬І»ЙЩКЎ·ЭІЙУГБЛЎ°![]() Ў±Ј¬Ў°
Ў±Ј¬Ў°![]() Ў±Ј¬Ў°
Ў±Ј¬Ў°![]() Ў±µИДЈКЅ.ЖдЦРЎ°
Ў±µИДЈКЅ.ЖдЦРЎ°![]() Ў±ДЈКЅµДІЩЧчУЦёьКЬ»¶УЈ¬јґУпКэНвИэГЕОЄ±ШїјїЖДїЈ¬И»єуФЪОпАнєНАъК·ЦРСЎїјТ»ГЕЈ¬ЧоєуґУКЈУаµДЛДГЕЦРСЎїјБЅГЕ.ДіРЈОЄБЛБЛЅвС§ЙъµДСЎїЖЗйїцЈ¬ґУёЯ¶юДкј¶µД2000ГыС§ЙъЈЁЖдЦРДРЙъ1100ИЛЈ¬Е®Йъ900ИЛЈ©ЦРЈ¬ІЙУГ·ЦІгійСщµД·Ѕ·ЁґУЦРійИЎnГыС§ЙъЅшРРµчІй.
Ў±ДЈКЅµДІЩЧчУЦёьКЬ»¶УЈ¬јґУпКэНвИэГЕОЄ±ШїјїЖДїЈ¬И»єуФЪОпАнєНАъК·ЦРСЎїјТ»ГЕЈ¬ЧоєуґУКЈУаµДЛДГЕЦРСЎїјБЅГЕ.ДіРЈОЄБЛБЛЅвС§ЙъµДСЎїЖЗйїцЈ¬ґУёЯ¶юДкј¶µД2000ГыС§ЙъЈЁЖдЦРДРЙъ1100ИЛЈ¬Е®Йъ900ИЛЈ©ЦРЈ¬ІЙУГ·ЦІгійСщµД·Ѕ·ЁґУЦРійИЎnГыС§ЙъЅшРРµчІй.
ЈЁ1Ј©ТСЦЄійИЎµДnГыС§ЙъЦРє¬ДРЙъ110ИЛЈ¬ЗуnµДЦµј°ійИЎµЅµДЕ®ЙъИЛКэЈ»
ЈЁ2Ј©ФЪЈЁ1Ј©µДЗйїцПВ¶ФійИЎµЅµДnГыН¬С§Ў°СЎОпАнЎ±єНЎ°СЎАъК·Ў±ЅшРРОКѕнµчІйЈ¬µГµЅПВБР2ЎБ2БРБЄ±н.ЗлЅ«БРБЄ±нІ№ідНкХыЈ¬ІўЕР¶ПКЗ·сУР99%µД°СОХИПОЄСЎїЖДїУлРФ±рУР№ШЈї
СЎОпАн | СЎАъК· | єПјЖ | |
ДРЙъ | 90 | ||
Е®Йъ | 30 | ||
єПјЖ |
ЈЁ3Ј©ФЪЈЁ2Ј©µДМхјюПВЈ¬ґУійИЎµДЎ°СЎАъК·Ў±µДС§ЙъЦР°ґРФ±р·ЦІгійСщФЩійИЎ5ГыЈ¬ФЩґУХв5ГыС§ЙъЦРійИЎ2ИЛБЛЅвСЎХюЦОЎўµШАнЎў»ЇС§ЎўЙъОпµДЗйїцЈ¬Зу2ИЛЦБЙЩУР1ГыДРЙъµДёЕВК.
ІОїј№«КЅЈє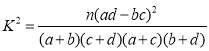 .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэfЈЁxЈ©![]() УлgЈЁxЈ©ЈЅ3elnx+mxµДНјПуУР4ёцІ»Н¬µДЅ»µгЈ¬ФтКµКэmµДИЎЦµ·¶О§КЗЈЁ Ј©
УлgЈЁxЈ©ЈЅ3elnx+mxµДНјПуУР4ёцІ»Н¬µДЅ»µгЈ¬ФтКµКэmµДИЎЦµ·¶О§КЗЈЁ Ј©
A.ЈЁ©Ѓ3Ј¬![]() Ј©B.ЈЁ©Ѓ1Ј¬
Ј©B.ЈЁ©Ѓ1Ј¬![]() Ј©C.ЈЁ©Ѓ1Ј¬3Ј©D.ЈЁ0Ј¬3Ј©
Ј©C.ЈЁ©Ѓ1Ј¬3Ј©D.ЈЁ0Ј¬3Ј©
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com