甲、乙两队在一次对抗赛的某一轮中有3个抢答题，比赛规定：对于每一个题，没有抢到题的队伍得0分，抢到题并回答正确的得1分，抢到题但回答错误的扣1分(即得－1分)；若X是甲队在该轮比赛获胜时的得分(分数高者胜)，则X的所有可能取值是________．
阅读快车系列答案科目：高中数学 来源：2015届贵州省高二下学期期中文科数学试卷（解析版） 题型：选择题
“
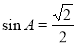”是“
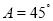”的（ ）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标3.2练习卷（解析版） 题型：填空题
对具有线性相关关系的变量x、y有观测数据(xi，yi)(i＝1,2，…，10)，它们之间的线性回归方程是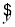
＝3x＋20，若
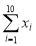＝18，则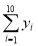
＝________.
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2章练习卷（解析版） 题型：解答题
学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．(每次游戏结束后将球放回原箱)
(1)求在一次游戏中，①摸出3个白球的概率，②获奖的概率；
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X)．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2章练习卷（解析版） 题型：填空题
在等差数列{an}中，a4＝2，a7＝－4.现从{an}的前10项中随机取数，每次取出一个数，取后放回，连续抽取3次，假定每次取数互不影响，那么在这三次取数中，取出的数恰好为两个正数和一个负数的概率为________(用数字作答)．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2章练习卷（解析版） 题型：填空题
在一次考试中，某班语文、数学、外语平均分在80分以上的概率分别为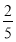
、
、
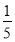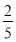，则该班的三科平均分都在80分以上的概率是________．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.6练习卷（解析版） 题型：解答题
已知某种零件的尺寸X(单位：mm)服从正态分布，其正态曲线在(0,80)上是增函数，在(80，＋∞)上是减函数，且f(80)＝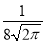
.
(1)求正态分布密度函数的解析式；
(2)估计尺寸在72mm～88mm之间的零件大约占总数的百分之几．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.5练习卷（解析版） 题型：解答题
某地位于甲、乙两条河流的交汇处，根据统计资料预测，今年汛期甲河流发生洪水的概率为0.25，乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响)．现有一台大型设备正在该地工作，为了保护设备，施工部门提出以下三种方案：
方案1：运走设备，此时需花费4000元；
方案2：建一保护围墙，需花费1000元，但围墙只能抵御一个河流发生的洪水，当两河流同时发生洪水时，设备仍将受损，损失约56000元；
方案3：不采取措施，此时，当两河流都发生洪水时损失达60000元，只有一条河流发生洪水时，损失为10000元．
(1)试求方案3中损失费X(随机变量)的分布列；
(2)试比较哪一种方案好．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.3练习卷（解析版） 题型：填空题
已知某种产品的合格率是95%，合格品中的一级品率是20%，则这种产品的一级品率为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
