在等差数列{an}中，a4＝2，a7＝－4.现从{an}的前10项中随机取数，每次取出一个数，取后放回，连续抽取3次，假定每次取数互不影响，那么在这三次取数中，取出的数恰好为两个正数和一个负数的概率为________(用数字作答)．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源：2015届贵州省高二下学期期中文科数学试卷（解析版） 题型：选择题
用反证法证明命题：“一个三角形中不能有两个直角”的过程归纳为以下三个步骤：
①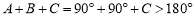
，这与三角形内角和为
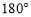相矛盾，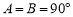
不成立；②所以一个三角形中不能有两个直角；③假设三角形的三个内角
、
、
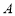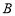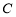中有两个直角，不妨设
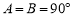；正确顺序的序号为 ( )
A．①②③ B．③①② C．①③② D．②③①
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标3.1练习卷（解析版） 题型：解答题
对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究，调查他们是否又发作过心脏病，调查结果如下所示：
| 又发作过心脏病 | 未发作过心脏病 | 合计 |
心脏搭桥手术 | 39 | 157 | 196 |
血管清障手术 | 29 | 167 | 196 |
合计 | 68 | 324 | 392 |
比较这两种手术对病人又发作心脏病的影响有没有差别．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2章练习卷（解析版） 题型：填空题
为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中微量元素x，y的含量(单位：毫克)．下表是乙厂的5件产品的测量数据：
编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 178 | 166 | 175 | 180 |
y | 75 | 80 | 77 | 70 | 81 |
(1)已知甲厂生产的产品共98件，求乙厂生产的产品数量；
(2)当产品中的微量元素x，y满足≥175且y≥75，该产品为优等品，用上述样本数据估计乙厂生产的优等品的数量；
(3)从乙厂抽出的上述5件产品中，随即抽取2件，求抽取的2件产品中优等品数X的分布列及其均值(即数学期望)．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2章练习卷（解析版） 题型：填空题
甲、乙两队在一次对抗赛的某一轮中有3个抢答题，比赛规定：对于每一个题，没有抢到题的队伍得0分，抢到题并回答正确的得1分，抢到题但回答错误的扣1分(即得－1分)；若X是甲队在该轮比赛获胜时的得分(分数高者胜)，则X的所有可能取值是________．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.6练习卷（解析版） 题型：解答题
若一批白炽灯共有10000只，其光通量X服从正态分布，其正态分布密度函数是f(x)＝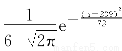
，x∈(－∞，＋∞)，试求光通量在下列范围内的灯泡的个数．
(1)(203,215)；(2)(191,227)．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.5练习卷（解析版） 题型：解答题
甲、乙两人各进行3次射击，甲每次击中目标的概率为
，乙每次击中目标的概率为
.
(1)求乙至多击中目标2次的概率；
(2)记甲击中目标的次数为Z，求Z的分布列、数学期望和标准差．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.3练习卷（解析版） 题型：填空题
已知A、B是相互独立事件，且P(A)＝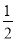
，P(B)＝
，则P(A
)＝________；P(
)＝________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，取得负数的概率为
，在三次取数中，取出的数恰好为两个正数和一个负数的概率为C32
2
1＝
.
＝0，则相关系数r＝________.