
| 解:(Ⅰ)f′(x)=3x2+2ax+b, 依题意,有: 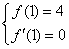 ,即 ,即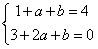 , ,解得: 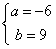 , ,所以,f(x)=x3-6x2+9x, f′(x)=3x2-12x+9=3(x-1)(x-3), 由f′(x)=0可得x=1或x=3, f′(x),f(x)在区间(0,4]上的变化情况为:
(Ⅱ)由函数的定义域是正数知,s>0,故极值点(3,0)不在区间[s,t]上; ①若极值点M(1,4)在区间[s,t]上,此时0<s≤1≤t<3, 故有(i) 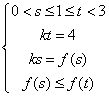 或(ii) 或(ii)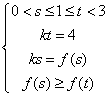 , ,(i)由k= 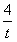 ,1≤t<3知,k∈( ,1≤t<3知,k∈(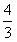 ,4],当且仅当t=1时,k=4; ,4],当且仅当t=1时,k=4;再由k=(s-3)2,0<s≤1知,k∈[4,9),当且仅当s=1时,k=4; 由于s≠t,故不存在满足要求的k值. (ii)由 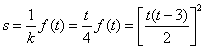 ,及0<s≤1可解得2≤t<3, ,及0<s≤1可解得2≤t<3,所以k= 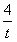 ,2≤t<3知,k∈( ,2≤t<3知,k∈(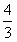 ,2]; ,2];即当k∈( 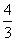 ,2]时,存在t= ,2]时,存在t=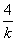 ∈[2,3), ∈[2,3),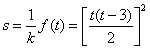 ∈(0,1], ∈(0,1],且f(s) ≥4s= 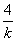 f(t) >f(t),满足要求。 f(t) >f(t),满足要求。②若函数f(x)在区间[s,t]上单调递增,则0<s<t<1或3<s<t,且 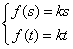 , ,故s,t是方程x2-6x+9=k的两根, 由于此方程两根之和为3,故[s,t]不可能同在一个单调增区间内; ③若函数f(x)在区间[s,t]上单调递减,则1<s<t<3, 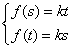 , ,两式相减并整理得s2(s-3)3=t2(t-3)2, 由1<s<t<3知s(s-3)=t(t-3),即s+t=3, 再将两式相减并除以s-t,得 -k=(s2+st+t2)-6(s+t)+9=(s+t)2-6(s+t)+9-st=-st,即k=st, 所以s,t是方程x2-3x+k=0的两根, 令g(x)=x2-3x+k, 则 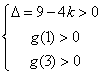 , ,解得2<k< 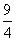 ,即存在s= ,即存在s=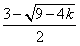 ,t= ,t=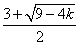 满足要求。 满足要求。综上可得,当 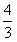 <k< <k<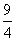 时,即k∈( 时,即k∈(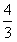 , ,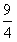 )时,存在两个不等正数s,t(s<t),使x∈[s,t]时,函数f(x)=x3-6x2+9x的值域恰好是[ks,kt]。 )时,存在两个不等正数s,t(s<t),使x∈[s,t]时,函数f(x)=x3-6x2+9x的值域恰好是[ks,kt]。 |


科目:高中数学 来源: 题型:
| 9 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| t-1 |
| 2 |
| t-1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 3 |
| x | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com