
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在 ![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() (
(![]() 是自然对数的底数)时,函数
是自然对数的底数)时,函数![]() 的最小值是
的最小值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)欲求在点![]() 处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
(2)先对函数![]() 进行求导,根据函数
进行求导,根据函数![]() 在[1,2]上是减函数可得到其导函数在[1,2]上小于等于0应该恒成立,再结合二次函数的性质可求得
在[1,2]上是减函数可得到其导函数在[1,2]上小于等于0应该恒成立,再结合二次函数的性质可求得![]() 的范围.
的范围.
(3)先假设存在,然后对函数![]() 进行求导,再对
进行求导,再对![]() 的值分情况讨论函数
的值分情况讨论函数![]() 在(0,e]上的单调性和最小值取得,可知当
在(0,e]上的单调性和最小值取得,可知当![]() =e2能够保证当
=e2能够保证当![]() 时
时![]() 有最小值3.
有最小值3.
试题解析:
(1)当![]() 时,
时, ![]()
所以![]() ,
, ![]()
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)因为函数在![]() 上是减函数,
上是减函数,
所以![]() 在[1,3]上恒成立.
在[1,3]上恒成立.
令![]() ,有
,有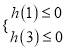 ,得
,得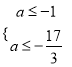
故![]() .
.
(3)假设存在实数a,使![]() 有最小值3,
有最小值3,
![]()
①![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
, ![]() (舍去)
(舍去)
②当![]() 时,
时, ![]() 在
在![]() 上恒成立, 所以
上恒成立, 所以![]() 在
在![]() 上单调递减,
上单调递减, ![]()
![]() (舍去)
(舍去)
③当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
所以![]() ,
, ![]() ,满足条件
,满足条件
综上,存在实数![]() ,使得
,使得![]()
![]() 时,
时, ![]() 有最小值3.
有最小值3.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为D,若对任意x1,x2∈D,当x1<x2时,都有
f(x1)≤f(x2),则称函数f(x)在D上为非减函数.设函数f(x)在[0,1]上为非减函数,且满足以下三个条件:①f(0)=0;②![]() ;③f(1-x)=2﹣f(x).则
;③f(1-x)=2﹣f(x).则![]() ( )
( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行的“国际马拉松赛”,举办单位在活动推介晚会上进行嘉宾现场抽奖活动,抽奖盒中装有6个大小相同的小球,分别印有“快乐马拉松”和“美丽绿城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球(取出后不再放回),若抽到的两个球都印有“快乐马拉松”标志即可获奖.并停止取球;否则继续抽取,第一次取球就抽中获一等奖,第二次取球抽中获二等奖,第三次取球抽中获三等奖,没有抽中不获奖.活动开始后,一位参赛者问:“盒中有几个印有‘快乐马拉松’的小球?”主持人说:“我只知道第一次从盒中同时抽两球,不都是‘美丽绿城行’标志的概率是
(1)求盒中印有“快乐马拉松”小球的个数;
(2)若用![]() 表示这位参加者抽取的次数,求
表示这位参加者抽取的次数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为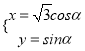 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及对应的点
的最小值及对应的点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() ,对任意实数
,对任意实数![]() 满足
满足![]() ,且函数
,且函数![]() 的最小值为2.
的最小值为2.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,其中
,其中![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]() ;
;
(3)若在区间![]() 上,函数
上,函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象上方,试确定实数
的图象上方,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调研,某超市一种玩具在过去一个月(按30天)的销售量(件)与价格(元)均为时间![]() (天)的函数,且销售量近似满足
(天)的函数,且销售量近似满足![]() ,价格近似满足
,价格近似满足![]() 。
。
(1)试写出该种玩具的日销售额![]() 与时间
与时间![]() (
(![]() ,
, ![]() )的函数关系式;
)的函数关系式;
(2)求该种玩具的日销售额![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列说法:

①AP⊥B1C;②BP与CD1所成的角是60°;③三棱锥![]() 的体积为定值;④B1P∥平面D1AC;⑤二面角P-AB-C的平面角为45°.
的体积为定值;④B1P∥平面D1AC;⑤二面角P-AB-C的平面角为45°.
其中正确说法的个数有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com