
设双曲线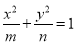 的离心率为2,且一个焦点与抛物线
的离心率为2,且一个焦点与抛物线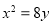 的焦点相同,则此双曲线的方程为__________.
的焦点相同,则此双曲线的方程为__________.
科目:高中数学 来源:2015届江苏省连云港高二下学期期末数学试卷(选修历史)(解析版) 题型:解答题
已知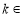 R且
R且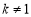 ,直线
,直线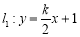 和
和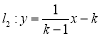 .
.
(1)求直线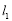 ∥
∥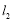 的充要条件;
的充要条件;
(2)当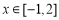 时,直线
时,直线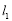 恒在x轴上方,求
恒在x轴上方,求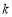 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考理科数学试卷(解析版) 题型:解答题
已知函数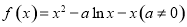 .
.
(1)求函数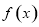 的单调区间;
的单调区间;
(2)若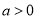 ,设
,设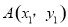 ,
, 是函数
是函数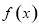 图像上的任意两点(
图像上的任意两点(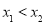 ),记直线AB的斜率为
),记直线AB的斜率为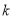 ,求证:
,求证: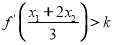 .
.
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考理科数学试卷(解析版) 题型:选择题
已知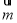
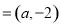 ,
,
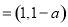 ,则 “a=2”是“
,则 “a=2”是“
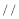
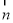 ”的( )
”的( )
A.充要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考文科数学试卷(解析版) 题型:解答题
如图甲,在平面四边形ABCD中,已知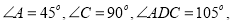
 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(1)求证:DC 平面ABC;
平面ABC;
(2)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.

查看答案和解析>>
科目:高中数学 来源:2015届广东省惠州市高三第二次调研考试理科数学试卷(解析版) 题型:选择题
设平面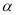 与平面
与平面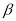 相交于直线
相交于直线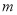 ,直线
,直线 在平面
在平面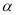 内,直线
内,直线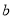 在平面
在平面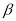 内,且
内,且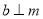 ,则“
,则“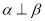 ”是“
”是“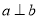 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com