
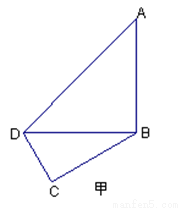
如图甲,在平面四边形ABCD中,已知
 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(1)求证:DC 平面ABC;
平面ABC;
(2)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.

(1)祥见解析;(2)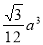 .
.
【解析】
试题分析:(1)先证明AB⊥底面BDC,可得AB⊥CD,又DC⊥BC,从而证明DC⊥平面ABC.
(2)由(1)知 EF⊥平面ABC,求得S△AEB=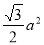 ,代入体积公式VA?BFE=VF?AEB=
,代入体积公式VA?BFE=VF?AEB=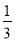 S△AEB•FE进行运算可得答案.
S△AEB•FE进行运算可得答案.
试题解析:(1)证明:在图甲中,∵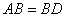 且
且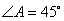
∴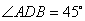 ,
,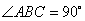 即
即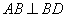 1分
1分
又在图乙中,∵平面ABD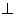 平面BDC ,且平面ABD
平面BDC ,且平面ABD 平面BDC=BD
平面BDC=BD
∴AB⊥底面BDC,∴AB⊥CD. 3分
∵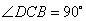 ,∴DC⊥BC 4分
,∴DC⊥BC 4分
又由 5分
5分
∴DC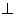 平面AB. 6分
平面AB. 6分
(2)∵点E、F分别为AC、AD的中点∴EF//CD 7分
又由(1)知,DC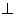 平面ABC
平面ABC
∴EF⊥平面ABC 8分
于是EF即为三棱锥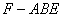 的高,∴
的高,∴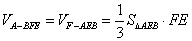 9分
9分
在图甲中,∵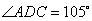 , ∴
, ∴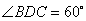 ,
,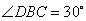
由 得
得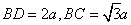 ,
,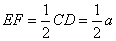 11分
11分
∴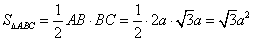 ∴
∴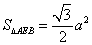 12分
12分
∴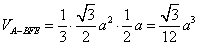 13分
13分
(若有其他解法,可视情况酌情给分)
考点:1.直线与平面垂直的判定;2.柱锥台的体积.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考理科数学试卷(解析版) 题型:填空题
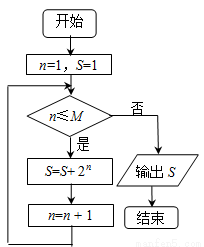
如图是一个算法的程序框图,若输出的结果是31,则判断框中的正整数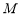 的值是___________.
的值是___________.
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考文科数学试卷(解析版) 题型:填空题
设双曲线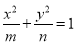 的离心率为2,且一个焦点与抛物线
的离心率为2,且一个焦点与抛物线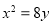 的焦点相同,则此双曲线的方程为__________.
的焦点相同,则此双曲线的方程为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com