
(本大题12分)
设函数f(x)= –cos2x–4tsin![]() cos
cos![]() +2t2–3t+4,xÎR,其中|t|≤1,将f(x)的最小值记为g(t)。
+2t2–3t+4,xÎR,其中|t|≤1,将f(x)的最小值记为g(t)。
(1)求函数g(t)的表达式;
(2)判断g(t)在[–1, 1]上的单调性,并求出g(t)的最值。
(1)因为函数f(x)= –cos2x–4tsin![]() cos
cos![]() +2t2–3t+4,xÎR,其中|t|≤1,
+2t2–3t+4,xÎR,其中|t|≤1,
所以f(x)=sin2x–2tsinx+2t2–3t+3=(sinx–t)2+ t2–3t+3…………………………3分
g(t)=f(x)min=f(t)= t2–3t+3………………………………………………6分
(2)g(t)= t2–3t+3=(t–![]() )2+
)2+![]() ,其对称轴为t=
,其对称轴为t=![]() ,开口向上,
,开口向上,
所以g(t)在[–1, 1]上的单调性为单调递减,………………………9分
g(t)min=1…………………………………………………………………………………11分
g(t)max=7…………………………………………………………………………………12分


科目:高中数学 来源:2011届四川省乐山一中高三上学期10月月考文科数学卷 题型:解答题
(本大题12分)设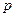 :实数
:实数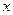 满足
满足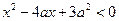 ,其中
,其中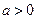 ,命题
,命题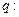 实数
实数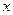 满足
满足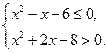 .
.
(Ⅰ)若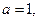 且
且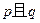 为真,求实数
为真,求实数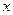 的取值范围;
的取值范围;
(Ⅱ)若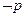 是
是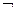
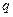 的充分不必要条件,求实数
的充分不必要条件,求实数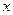 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三上学期10月月考文科数学卷 题型:解答题
(本大题12分)设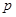 :实数
:实数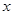 满足
满足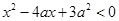 ,其中
,其中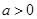 ,命题
,命题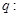 实数
实数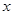 满足
满足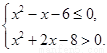 .
.
(Ⅰ)若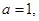 且
且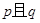 为真,求实数
为真,求实数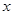 的取值范围;
的取值范围;
(Ⅱ)若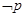 是
是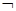
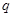 的充分不必要条件,求实数
的充分不必要条件,求实数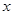 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com