
科目:高中数学 来源:2016届江西省高三上学期第三次考试理科数学试卷(解析版) 题型:解答题
已知等差数列 满足:
满足: ,
, ,其中
,其中 为数列
为数列 的前n项和.
的前n项和.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若Equation Section (Next) ,且
,且 成等比数列,求
成等比数列,求 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2015-2016学年广东省清远市实验学校高二上学期期中数学试卷(解析版) 题型:选择题
对于任意实数a、b、c、d,命题① ;②
;②
③ ;④
;④ ;⑤
;⑤ .
.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省扶余市高二上学期期中考试文科数学试卷(解析版) 题型:解答题
已知数列 的通项公式为
的通项公式为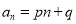 ,其中
,其中 为常数,那么这个数列一定是等差数列吗?证明你的结论。
为常数,那么这个数列一定是等差数列吗?证明你的结论。
查看答案和解析>>
科目:高中数学 来源:2015-2016学年福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分) 在△ABC中,a,b,c分别是角A,B,C的对边,且 .
.
(1)求角B的大小;
(2)若 ,求实数b的取值范围.
,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省赣州市十三县高二上期中联考文科数学试卷(解析版) 题型:选择题
公元前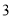 世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(
世纪,古希腊欧几里得在《几何原本》里提出:“球的体积( )与它的直径(
)与它的直径(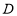 )的立方成正比”,此即
)的立方成正比”,此即 ,欧几里得未给出
,欧几里得未给出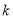 的值.
的值.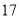 世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式
世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式 中的常数
中的常数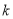 称为“立圆率”或“玉积率
称为“立圆率”或“玉积率 ”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式
”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式 求体
求体 积(在等边圆柱中,
积(在等边圆柱中,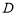 表示底面圆的直径;在正方体中,
表示底面圆的直径;在正方体中,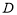 表示棱长).假设运用此体积公式求得球(直径为
表示棱长).假设运用此体积公式求得球(直径为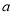 )、等边圆柱(底面圆的直径为
)、等边圆柱(底面圆的直径为 )、正方体(棱长为
)、正方体(棱长为 )的“玉积率”分别为
)的“玉积率”分别为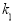 、
、 、
、 ,那么
,那么 ( )
( )
A.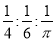 B.
B.
C.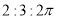 D.
D.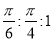
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com