
【题目】在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上异于
上异于![]() 的一点,光线从点
的一点,光线从点![]() 出发,经
出发,经![]() 反射后又回到原点
反射后又回到原点![]() ,光线
,光线![]() 经过
经过![]() 的重心.
的重心.
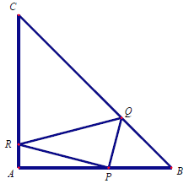
(1)建立适当的坐标系,请求![]() 的重心
的重心![]() 的坐标;
的坐标;
(2)求点![]() 的坐标;
的坐标;
(3)求![]() 的周长及面积.
的周长及面积.
【答案】(1)坐标系见解析,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]()
![]()
【解析】
(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立直角坐标系,依次写出
轴建立直角坐标系,依次写出![]() 的坐标,由重心公式求得重心即可;
的坐标,由重心公式求得重心即可;
(2)由光的反射具有对称性,作![]() 关于
关于![]() 的对称点
的对称点![]() ,关于
,关于![]() 的对称点
的对称点![]() ,则
,则![]() 四点共线,设
四点共线,设![]() ,根据对称性可得
,根据对称性可得![]() ,
,![]() ,且
,且![]() 在直线
在直线![]() 上,解出
上,解出![]() 方程并将点
方程并将点![]() 坐标代入即可求得
坐标代入即可求得![]() ,进而得到
,进而得到![]() 的坐标;
的坐标;
(3)由(2), ![]() 的周长转化为
的周长转化为![]() 的长,利用割补法将
的长,利用割补法将![]() 的面积转化为
的面积转化为![]() 的面积与
的面积与![]() 的面积的差计算即可
的面积的差计算即可
(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立直角坐标系,则
轴建立直角坐标系,则![]() ,
,![]() ,
,![]() ,
,
所以根据重心公式可得重心![]() 为
为![]() ,即
,即![]()
(2)作![]() 关于
关于![]() 的对称点
的对称点![]() ,关于
,关于![]() 的对称点
的对称点![]() ,由于光的反射原理,
,由于光的反射原理,![]() 四点共线,
四点共线,
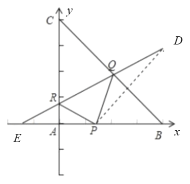
因为![]() 过重心
过重心![]() ,所以
,所以![]() 过重心
过重心![]() ,
,
设![]() ,则
,则![]() ,
,
因为![]() ,
,![]() ,所以直线
,所以直线![]() 为:
为:![]() ,
,
设![]() ,则
,则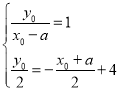 ,所以
,所以 ,即
,即![]()
则直线![]() 为
为![]() ,
,
由(1),代入点![]() ,即
,即![]() ,
,
所以![]() 或
或![]() ,
,
因为![]() 异于
异于![]() ,
,
所以点![]() 为
为![]()
(3)由(2),![]() ,
,![]() ,
,
由于对称性,则![]() 的周长为:
的周长为: ,
,
直线![]() 为
为 ,即
,即![]() ,
,
当![]() 时,
时,![]() ,则
,则![]()
联立![]() ,解得
,解得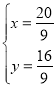 ,则
,则![]() ,
,
所以![]() 的面积为:
的面积为:![]()
![]()
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列有关平面向量分解定理的四个命题:
(1)一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基;
(2)一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基;
(3)平面向量的基向量可能互相垂直;
(4)一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.
其中正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() , 如图(2).
, 如图(2).

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABD﹣A1B1C1D1中四边形A1B1C1D1,ADD1A1.ABB1A1均为正方形.点M是BD的中点.点H在线段C1M上,且A1H与平面ABD所成角的正弦值为![]() .
.
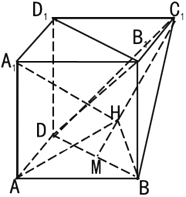
(Ⅰ)证明:B1D1∥平面BC1D:
(Ⅱ)求二面角A﹣A1H﹣B的的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下三个命题:
①若![]() ,则
,则![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() ;
;
③在一元二次方程![]() 中,若
中,若![]() ,则方程有实数根.
,则方程有实数根.
其中原命题、逆命题、否命题、逆否命题均为真命题的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P是椭圆![]() 上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
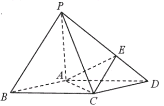
(1)证明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥?证明你的结论.
是正三棱锥?证明你的结论.
(3)求以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角
为面的二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com