
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() , 如图(2).
, 如图(2).

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出![]() ,
,![]() ,从而
,从而![]() 面
面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;
;
(2)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,则
,则![]() 面
面![]() ,以
,以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,利用向量法能求出平面
轴建立空间直角坐标系,利用向量法能求出平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)证明:![]() 四边形
四边形![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的两个三等分点,
的两个三等分点,
![]() 四边形
四边形![]() 是正方形,
是正方形,![]()
![]() ,
,
![]()
![]() ,且
,且![]() ,
,![]()
![]() 面
面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,则
,则![]() 面
面![]() ,
,
以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,如图所示:
轴建立空间直角坐标系,如图所示:
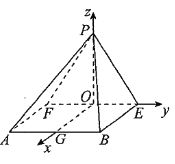
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则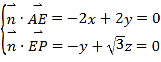 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则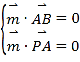 ,∴
,∴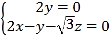 ,取
,取![]() ,得:
,得:![]() ,
,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,
,
则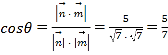 .
.
![]() 平面
平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
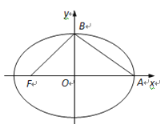
【题目】已知椭圆![]() ,
,![]() 、
、![]() 分别是椭圆短轴的上下两个端点;
分别是椭圆短轴的上下两个端点;![]() 是椭圆的左焦点,P是椭圆上异于点
是椭圆的左焦点,P是椭圆上异于点![]() 、
、![]() 的点,
的点,![]() 是边长为4的等边三角形.
是边长为4的等边三角形.
(1)写出椭圆的标准方程;
(2)设点R满足:![]() ,
,![]() .求证:
.求证:![]() 与
与![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,右顶点为B,且满足
,右顶点为B,且满足![]()
![]() Ⅰ
Ⅰ![]() 求椭圆的离心率e;
求椭圆的离心率e;
![]() Ⅱ
Ⅱ![]() 设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点
设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点![]() ,问是否存在过
,问是否存在过![]() 的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二阶方矩阵![]() ,则矩阵
,则矩阵![]() 所对应的矩阵变换为:
所对应的矩阵变换为:![]() ,其意义是把点
,其意义是把点![]() 变换为点
变换为点![]() ,矩阵
,矩阵![]() 叫做变换矩阵.
叫做变换矩阵.
(1)当变换矩阵![]() 时,点
时,点![]() 、
、![]() 经矩阵变换后得到点分别是
经矩阵变换后得到点分别是![]() 、
、![]() ,求经过点
,求经过点![]() 、
、![]() 的直线的点方向式方程;
的直线的点方向式方程;
(2)当变换矩阵![]() 时,若直线上的任意点
时,若直线上的任意点![]() 经矩阵变换后得到的点
经矩阵变换后得到的点![]() 仍在该直线上,求直线的方程;
仍在该直线上,求直线的方程;
(3)若点![]() 经过矩阵
经过矩阵![]() 变换后得到点
变换后得到点![]() ,且
,且![]() 与
与![]() 关于直线
关于直线![]() 对称,求变换矩阵
对称,求变换矩阵![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度![]() (单位:cm)的情况如表1:
(单位:cm)的情况如表1:
| 900 | 700 | 300 | 100 |
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年11月份AQI指数频数分布如表2:
|
|
|
|
|
|
频数(天) | 3 | 6 | 12 | 6 | 3 |
<>(1)设
(2)小李在该市开了一家洗车店,洗车店每天的平均收入与AQI指数存在相关关系如表3:
|
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
根据表3估计小李的洗车店2017年11月份每天的平均收入.
附参考公式:![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
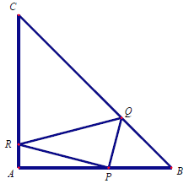
【题目】在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上异于
上异于![]() 的一点,光线从点
的一点,光线从点![]() 出发,经
出发,经![]() 反射后又回到原点
反射后又回到原点![]() ,光线
,光线![]() 经过
经过![]() 的重心.
的重心.
(1)建立适当的坐标系,请求![]() 的重心
的重心![]() 的坐标;
的坐标;
(2)求点![]() 的坐标;
的坐标;
(3)求![]() 的周长及面积.
的周长及面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .
.
(1)已知椭圆的离心率为![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)已知△![]() 外接圆的圆心在直线
外接圆的圆心在直线![]() 上,求椭圆的离心率
上,求椭圆的离心率![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com