
【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度![]() (单位:cm)的情况如表1:
(单位:cm)的情况如表1:
| 900 | 700 | 300 | 100 |
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年11月份AQI指数频数分布如表2:
|
|
|
|
|
|
频数(天) | 3 | 6 | 12 | 6 | 3 |
<>(1)设
(2)小李在该市开了一家洗车店,洗车店每天的平均收入与AQI指数存在相关关系如表3:
|
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
根据表3估计小李的洗车店2017年11月份每天的平均收入.
附参考公式:![]() ,其中
,其中 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工一件甲所需工时分别为1![]() ,2
,2![]() ,加工一件乙设备所需工时分别为2
,加工一件乙设备所需工时分别为2![]() ,1
,1![]() .A、B两种设备每月有效使用台时数分别为400
.A、B两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,分别用
,分别用![]() 表示计划每月生产甲,乙产品的件数.
表示计划每月生产甲,乙产品的件数.
(Ⅰ)用![]() 列出满足生产条件的数学关系式,并画出相应的平面区域;
列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种产品各多少件,可使收入最大?并求出最大收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() -
-![]() =1(a>0,b>0)的离心率为2,焦点到渐近线的距离等于
=1(a>0,b>0)的离心率为2,焦点到渐近线的距离等于![]() ,过右焦点F2的直线l交双曲线于A,B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A,B两点,F1为左焦点.
(1)求双曲线的方程;
(2)若△F1AB的面积等于6![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)已知![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)已知![]() ,设
,设![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,且
的两根,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)已知![]() 满足
满足![]() ,且关于
,且关于![]() 的方程
的方程![]() 的两实数根分别在区间
的两实数根分别在区间![]() 内,求实数
内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]()
![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() .
.
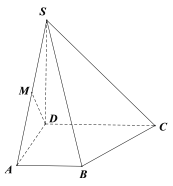
(Ⅰ)证明:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 平面
平面![]() . 若存在,确定
. 若存在,确定![]() 点的位置;若不存在,说明理由.
点的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市周年庆典,设置了一项互动游戏如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头![]() 所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头
所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头![]() 指向每个区域的可能性都是相等的.要求每个家庭派一名儿童和一位成人先后各转动一次游戏转盘,记为
指向每个区域的可能性都是相等的.要求每个家庭派一名儿童和一位成人先后各转动一次游戏转盘,记为![]() ,若一个家庭总得分
,若一个家庭总得分![]() ,假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动,游戏规定:
,假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动,游戏规定:

①若![]() ,则该家庭可以获得一等奖一份;
,则该家庭可以获得一等奖一份;
②若![]() ,则该家庭可以获得二等奖一份;
,则该家庭可以获得二等奖一份;
若![]() ,则该家庭可以获得纪念奖一份.
,则该家庭可以获得纪念奖一份.
(1)求一个家庭获得纪念奖的概率;
(2)试比较同一个家庭获得一等奖和二等奖概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 在
在![]() 上的最小值(
上的最小值(![]() 为自然对数的底数);
为自然对数的底数);
(3)是否存在实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 均成立?若存在,求出所有满足条件的实数
均成立?若存在,求出所有满足条件的实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.

(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com