
【题目】如图,A、B、C、D为平面四边形ABCD的四个内角.
(1)证明:tan ![]() ;
;
(2)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() 的值.
的值.
【答案】
(1)证明: tan ![]() =
= ![]() =
= 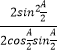 =
= ![]() .等式成立.
.等式成立.
(2)解:由A+C=180°,得C=180°﹣A,D=180°﹣B,由(Ⅰ)可知:tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() =
= ![]() =
= ![]() ,连结BD,在△ABD中,有BD2=AB2+AD2﹣2ABADcosA,AB=6,BC=3,CD=4,AD=5,
,连结BD,在△ABD中,有BD2=AB2+AD2﹣2ABADcosA,AB=6,BC=3,CD=4,AD=5,
在△BCD中,有BD2=BC2+CD2﹣2BCCDcosC,
所以AB2+AD2﹣2ABADcosA=BC2+CD2﹣2BCCDcosC,
则:cosA= ![]() =
= ![]() =
= ![]() .
.
于是sinA= ![]() =
= ![]() ,
,
连结AC,同理可得:cosB= ![]() =
= ![]() =
= ![]() ,
,
于是sinB= ![]() =
= ![]() .
.
所以tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)直接利用切化弦以及二倍角公式化简证明即可.(2)通过A+C=180°,得C=180°﹣A,D=180°﹣B,利用(1)化简tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() =
= ![]() ,连结BD,在△ABD中,利用余弦定理求出sinA,连结AC,求出sinB,然后求解即可.
,连结BD,在△ABD中,利用余弦定理求出sinA,连结AC,求出sinB,然后求解即可.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
【题目】已知点A(x1,y1),B(x2,y2),M(1,0),![]() =(3λ,4λ)(λ≠0),
=(3λ,4λ)(λ≠0),![]() =-4
=-4![]() ,若抛物线y2=ax经过A和B两点,则a的值为( )
,若抛物线y2=ax经过A和B两点,则a的值为( )
A. 2 B. -2
C. -4 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f (x)=(x+1)lnx﹣a (x﹣1)在x=e处的切线与y轴相交于点(0,2﹣e).
(1)求a的值;
(2)函数f (x)能否在x=1处取得极值?若能取得,求此极值;若不能,请说明理由.
(3)当1<x<2时,试比较 ![]() 与
与 ![]() 大小.
大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P(3,0)在圆C:(x﹣m)2+(y﹣2)2=40内,动直线AB过点P且交圆C于A、B两点,若△ABC的面积的最大值为20,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x﹣1|﹣2|x+1|的最大值为m.
(1)求m;
(2)若a,b,c∈(0,+∞),a2+2b2+c2=m,求ab+bc的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(1,-3,2),
=(1,-3,2),![]() =(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求|2![]() +
+![]() |;
|;
(2)在直线AB上,是否存在一点E,使得![]() ⊥
⊥ ![]() ?(O为原点)
?(O为原点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com