| 解:(1)设点A、B的坐标分别为(x1,y1)、(x2,y2),点Q的坐标为Q(x,y).
当x1≠x2时,设直线斜率为k,则l的方程为y=k(x-a)+b.
由已知x12+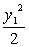 =1 ①,x22+ =1 ①,x22+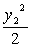 =1 ② =1 ②
y1=k(x1-a)+b ③,y2=k(x2-a)+b ④
①-②得(x1+x2)(x1-x2)+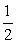 (y1+y2)(y1-y2)=0.
⑤ (y1+y2)(y1-y2)=0.
⑤
③+④得y1+y2=k(x1+x2)-2ka+2b ⑥
由⑤、⑥及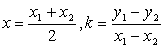 , ,
得点Q的坐标满足方程2x2+y2-2ax-by=0 ⑦
当x1=x2时,k不存在,此时l平行于y轴,因此AB的中点Q一定落在x轴,即Q的坐标为(a,0),显然点Q的坐标满足方程⑦
综上所述,点Q的坐标满足方程2x2+y2-2ax-by=0.
设方程⑦所表示的曲线为l.
则由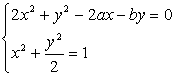 得(2a2+b2)x2-4ax+2-b2=0. 得(2a2+b2)x2-4ax+2-b2=0.
因为Δ=8b2(a2+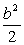 -1),由已知a2+ -1),由已知a2+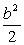 ≤1 ≤1
所以当a2+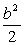 =1时,Δ=0,曲线l与椭圆C有且只有一个交点P(a,b); =1时,Δ=0,曲线l与椭圆C有且只有一个交点P(a,b);
当a2+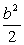 <1时,Δ<0,曲线l与椭圆C没有交点. <1时,Δ<0,曲线l与椭圆C没有交点.
因为(0,0)在椭圆C内,又在曲线l上,所以曲线l在椭圆C内.
故点Q的轨迹方程为2x2+y2-2ax-by=0;
(2)由 ,得曲线l与y轴交于点(0,0)、(0,b); ,得曲线l与y轴交于点(0,0)、(0,b);
由 ,得曲线l与x轴交于点(0,0)、(a,0); ,得曲线l与x轴交于点(0,0)、(a,0);
当a=0,b=0,即点P(a,b)为原点时,(a,0)、(0,b)与(0,0)重合,曲线l与x轴只有一个交点(0,0);
当a=0且0<|b|≤ 时,即点P(a,b)不在椭圆C外且在除去原点的y轴上时,点(a,0)与(0,0)重合,曲线l与坐标轴有两个交点(0,b)与(0,0); 时,即点P(a,b)不在椭圆C外且在除去原点的y轴上时,点(a,0)与(0,0)重合,曲线l与坐标轴有两个交点(0,b)与(0,0);
同理,当b=0且0<|a|≤1时,即点P(a,b)不在椭圆C外且在除去原点的x轴上时,曲线l与坐标轴有两个交点(a,0)与(0,0);
当0<|a|<1且0<|b|<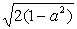 时,即点P(a,b)在椭圆C内且不在坐标轴上时,曲线l与坐标轴有三个交点(a,0)、(0,b)与(0,0). 时,即点P(a,b)在椭圆C内且不在坐标轴上时,曲线l与坐标轴有三个交点(a,0)、(0,b)与(0,0).
| 

