练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设数列的前项和为，且对任意正整数，满足．

    （1）求数列的通项公式．

    （2）设，求数列的前项和．

    【答案】（1）；（2）．

    【解析】

    试题分析：（1）由当时，，两式相减得

    ．又当时，

    是以首项，公比的等比数列的通项公式为；（2）由（1）知， ．

    试题解析： （1）因为，

    所以，当时，，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分

    两式相减得，即．．．．．．．．．．．．．．．．3分

    又当时，，即．．．．．．．．．．4分

    所以是以首项，公比的等比数列，

    所以数列的通项公式为．．．．．．．．．．．．．．．．．．．．．．．6分

    （2）由（1）知，，．．．．．．．．．．．．．．．．．．．7分

    则，①

    ，②．．．．．．．．．．．．．．．．．8分

    ②-①得

    ，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分

    ，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．11分

    所以，数列的前项和为．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】轮船由甲地逆水匀速行驶至乙地，甲、乙两地相距s(km)，水流速度为p(km/h)，轮船在静水中的最大速度为q(km/h)(p，q为常数，且q>p)，已知轮船每小时的燃料费用与轮船在静水中的速度v(km/h)成正比，比例系数为常数k.

    (1)将全程燃料费用y(元)表示为静水中速度v(km/h)的函数；

    (2)若s＝100，p＝10，q＝110，k＝2，为了使全程的燃料费用最少，轮船的实际行驶速度应为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知随机变量的取值为不大于的非负整数值，它的分布列为：

    0

    1

    2

    n

    其中（）满足： ，且．

    定义由生成的函数，令．

    （I）若由生成的函数，求的值；

    （II）求证：随机变量的数学期望， 的方差；

    （）

    （Ⅲ）现投掷一枚骰子两次，随机变量表示两次掷出的点数之和，此时由生成的函数记为，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了研究家用轿车在高速公路上的车速情况，交通部门随机对50名家用轿车驾驶员进行调查，得到其在高速公路上行驶时的平均车速情况为：在30名男性驾驶员中，平均车速超过的有20人，不超过的有10人.在20名女性驾驶员中，平均车速超过的有5人，不超过的有15人.

    （Ⅰ）完成下面的列联表，并判断是否有的把握认为平均车速超过的人与性别有关；

    平均车数超过

    人数

    平均车速不超过

    人数

    合计

    男性驾驶员人数

    女性驾驶员人数

    合计

    （Ⅱ）以上述数据样本来估计总体，现从高速公路上行驶的大量家用轿车中随即抽取3辆，记这3辆车中驾驶员为女性且车速不超过的车辆数为，若每次抽取的结果是相互独立的，求的分布列和数学期望

    参考公式：，其中.

    参考数据：

    0.150

    0．100

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班从6名班干部中（其中男生4人，女生2人），任选3人参加学校的义务劳动．

    （1）设所选3人中女生人数为ξ，求ξ的分布列；

    （2）求男生甲或女生乙被选中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】集合A={x|ax2-2x+2=0},集合B={y|y2-3y+2=0},如果AB,求实数a的取值集合..

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）将函数的图像向右平移个单位得到函数的图像，若，求函数的值域；

    （2）已知，分别为中角的对边，且满足，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC－A1B1C1中，△ABC是等边三角形，BC＝CC1＝4，D是A1C1中点．

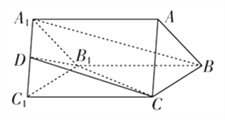
    (1)求证：A1B∥平面B1CD；

    (2)当三棱锥C－B1C1D体积最大时，求点B到平面B1CD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

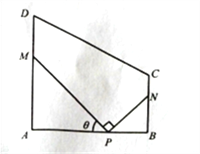
    【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC, 百米， 百米，广场入口P在AB上，且，根据规划，过点P铺设两条相互垂直的笔直小路PM,PN（小路的宽度不计），点M,N分别在边AD,BC上（包含端点），区域拟建为跳舞健身广场， 区域拟建为儿童乐园，其它区域铺设绿化草坪，设.

    （1）求绿化草坪面积的最大值；

    （2）现拟将两条小路PNM,PN进行不同风格的美化，PM小路的美化费用为每百米1万元，PN小路的美化费用为每百米2万元，试确定M,N的位置，使得小路PM,PN的美化总费用最低，并求出最小费用.

    查看答案和解析>>

    同步练习册答案